Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Править]Свойства

§ По теореме о гранях для любого ограниченного сверху подмножества 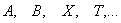, существует .

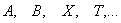§ По теореме о гранях для любого ограниченного снизу подмножества 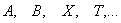, существует .

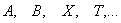§ Вещественное число 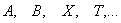является 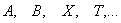тогда и только тогда, когда

1. 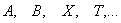есть верхняя грань 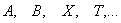то есть для всех элементов , .

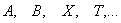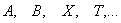2. для любого 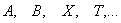найдётся 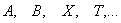, такой, что 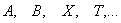(то есть к 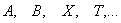можно сколь угодно «близко подобраться» из множества )

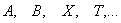§ Аналогичное утверждение верно для точной нижней грани.

4.ПРИНЦИП ВЕРХНЕЙ ГРАНИ.

Принцип верхней грани: всякое непустое, ограниченное сверху подмножество множества действительных чисел обладает точной верхней границей и при том единственной.

5.Принцип Архимеда и следствие из него.

1.71. Если х—вещественное число, а п—целое число, то числа пх называются целыми кратными х.

Принцип Архимеда**). Если х > 0, а у—произ­вольное вещественное число, то существует такое целое крат­ное пх числа х, для которого (п — 1) хпх >у.

Доказательство. Предположим, что для всех целых р выполняется неравенство рх^.у. Это значит, что множе­ство А всех чисел {рх} ограничено и имеет число у своей верхней гранью. По аксиоме 1.24 существует точная верхняя грань множества {рх}, | = sup А Число | — х < | уже не яв­ляется верхней гранью множества А; поэтому существует та­кое/?, что рх > £—х. Отсюда (p-j- 1) х > £ и | не может быть верхней гранью множества А. Полученное противоречие доказывает существование целого числа р, для которого рх >_у. Аналогично существует целое число q, для которого qx<y; очевидно, q^Lp. Перебирая все пары (q, #+!)> (q-{-1, q-\-2),..., (р — 1, jo), найдем среди них такую, например (п—1, п), для которой (п—a nxi>y.

*) Для таких множеств предлагались в свое время названия «интрезок» и «оттервал», однако при всей их целесообразности в оби­ход они ие вошли.

**) В других современных аксиоматических теориях веществен­ных чисел принцип Архимеда, наряду с принципом Кантора (§ 1.8), входит в состав аксиом; при таком построении аксиома о верхней грани (1.24) становится теоремой.

В частности, если х = 1, мы получаем, что для любого y£R существует такое целое л, что п — 1 < п. Число п—1 называется целой частью числа у и обозначается [у]. Число у—[у] называется дробной частью числа у и обозна­чается (_у). Таким образом, всякое число у есть сумма своей целой части и своей дробной части: у= [у] +

1.72. Заменяя всюду в 1.71 сложение умножением, полу­чаем следующий мультипликативный*) вариант принципа Архимеда:

Если х > 1, у > 0, то существует такой целый показа­тель п, что

дхп>у.

1.73. Если в условии принципа Архимеда число у также положительно, то положительно и число п > —. Умножая

' X

X

последнее неравенство на —, приходим к следующему за­ключению:

Для любых х > 0 и у > 0 существует такое натуральное

число п, что — < х. ' п

Как следствие получаем: при любом у > 0

inf|-|-, я=1, 2,...|=0. (1)

Действительно, множество в скобках состоит из положи­тельных чисел, поэтому его нижняя грань неотрицательна. Но по * доказанному она не может быть положительной; отсюда вытекает (1).

1.74. Следствие. Каждая из систем полуоткрытых промежутков

(0, y]z> (о, I] з... з (о,... СУ >0), (1)

(а, в-Ку]э(а, в + -|]э...=з («,«+!"]=>■••, (2)

[Й—у, a) Z) ^Й—, Й) =>... =>[°—jp (3)

имеет пустое пересечение.

*) От слова multiplicator—умножающий (лат.).

Действительно, если бы промежутки системы (2) имели общую точку то |—а была бы общей точкой системы (1); и если бы промежутки системы (3) имели общую точку г], то а—к] была бы общей точкой системы (1). Но промежутки системы (1) не могут иметь ни одной общей точки в силу 1.73, что и доказывает утверждение.

1.75. Теорема. Каждый интервал (а, Ь) содержит рациональную точку.

Доказательство. Пусть h = b—с> О и п—'Целое,

большее, чем (существующее по принципу Архимеда)', так

что -i- < h. По принципу Архимеда найдется такое т, что

т - „т+1 л т+1 1.,

— <С «<" —-—. При этом a sC — < b — а, так что

п — п г п ■ п '

< Ь. Таким образом, а < —< Ь, € (я. Ь), что

и требовалось.

На самом деле между а и b существует даже бесконеч­ное множество рациональных чнсел, поскольку, применяя

приведенное рассуждение к интервалу I ^, b), мы полу­чим новое рациональное число, ^ у < Ь, и про­цесс можно продолжать неограниченно.

1.76. Для заданного вещественного числа | обозначим через N% совокупность всех рациональных чисел

и через */>£ совокупность всех рациональных чисел Множествоограничено сверху (числом £), множество Р^ ограничено снизу (числом |). Теорема, supN^ = | = inf

Доказательство. Пусть supA^ = a. Так как для каждого s £ Nr, то по определению точной верхней грани имеем Предположим, что а<|. По 1.75 имеется

рациональная точка р£(а, Так как р < то откуда вытекает p^supA^=a, что противоречит включе­нию р£(а, £). Следовательно, неравенство а<£ невоз­можно, откуда a = supA^ = |. Аналогично доказывается, что 1 = МРГ

1.77. Позиционная десятичная запись веще­ственных чисел. Мы проверим здесь, что с помощью последовательности из знаков 0, 1, 2,..., 9 можно запи­сать любое вещественное число. Положим 9+ 1 = 10.

Пусть £>0. В силу 1.72 существует (и однозначно определен) такой показатель р, что

10Р<£< 10Р+1.

Имея р, найдем число 0О (из набора 1, 2,..,,9) такое, что

е0.юр<£<(е0+1).1оя.

Число 60 также определено однозначно, так как промежутки в-lOf < (8 + 1)-10я

при различных 6 = 0, 1,..., 9 не пересекаются. Далее, имея 60, найдем число 6Х (из набора 0, 1, 2,..., 9) такое, что

е0 • 1 о?+ех • 1 оя -1 < ^ < е0 • 1 оя+(вх-f 1). 1 оя-1.

Продолжая этот процесс неограниченно, мы получим после­довательность символов (цифр от 0 до 9)

еле,... (0Оф0). (1)

Для указания числа р поступаем так: если р ^ 0, ставим запятую между символами и 6р+1; если р < 0, т. е. р = —<7, q > 0, перед последовательностью (1) пишем до­полнительно q нулей и после первого из них ставим запя­тую. С учетом этого условия в записи отражено и число р.

Итак, каждому вещественному числу | мы поставили в соответствие по указанному правилу символ вида (1), воз­можно, с несколькими нулями впереди и с запятой на неко­тором месте. Этот символ называется десятичной позицион­ной записью числа цифры 60, вх,... в их взаимных положениях (позициях) в последовательности (1) называются десятичными знаками числа Для числа 1 десятичная запись имеет вид 1,000...; аналогичный вид имеет десятич­ная запись для чисел 2, 3,..., 9. Для числа 10 десятич-

§

ная запись имеет вид 10,000... Для чисел вида —- с не­

отрицательными целыми s и t («десятично рациональных») и только для них в символе (1) не более чем t цифр после запятой отлично от 0.

Мы утверждаем, что в символе (1) не может быть так, что, начиная с некоторого места, все цифры являются девятками. Действительно, наличие всех девяток, начиная с номера п после запятой, означало бы, что число | лежит в промежутках

Г~Г JOn^s ь Г~Т~ ДОИ Г1 IQn-l»

9 9 у 9 10 _1

r+10»+10»+i^fc ^ Г~>~10" 10"+1 10"-1 '

Г+10«+ 10"+1+" • + + 10"-1'

но все вместе эти промежутки не имеют ни одной общей точки (1.74).

Обратно, пусть дана произвольная последовательность цифр от 0 до 9

т^... (2)

с запятой на некотором месте, причем не все xt суть нули и как угодно далеко имеются цифры, отличные от 9. Пока­жем,- что существует число £>0, для которого (2) совпадает с представляющим его символом (1).

Пусть хт—первая отличная от 0 цифра в (2). Запятая находится или правее хт на q ^ 0 цифр (не считая хт), или левее хт на t ^ 1 цифр (считая хт); во втором случае по­ложим q = —t. Теперь положим

| = sup {10?.Tm + l^.T^-f 10?"2-тт+2+... +

и покажем, что десятичное разложение этого числа | сов­падает с (2). Пусть фиксировано натуральное число s, затем

выбрано г > s так, чтобы хт+г ^8, и пусть k > г произ­вольно. Тогда, суммируя геометрическую прогрессию, найдем

10?~(i+1)-tra+i+14-... + 10»-'.ти+,+... + <

<^9-109"w+1) +... -f-9-109-r+... +9-10?-*—10«-'- =

„ 109-<'у+1>—109-(ft+1) = 9 • ——1 —ю-i 109-' < —

Поэтому

£ = sup {10»-тю +... + 10»-*.ти+,+... + \W~*-xm+k} <

< 10»-т„+... + 10»"*-tffi+.,+ 10»-'— 10»-' < <10».ти+... + 10»-*(ти+, + 1).

Итак, при любом s = 0, 1, 2,... 10».ти+... + 10»-*.ти+,<1<

Полагая здесь s = 0, 1, 2,... и вспоминая определение числа р и знаков 80, 81,... числа мы находим p±=q, — тт> 01 — •-■■> откуда н следует совпадение Деся­

тичного разложения числа \ с символом (2). Если |< 0, то —\ > 0, и поэтому

— 1 = г1т2...,

как было показано выше; мы полагаем по определению

| = _tlt2... Наконец, для | = 0 мы полагаем

1 = 0,0000...

Этим завершается построение позиционной десятичной системы.

1.78. Вместо числа 10 можно взять какое-либо другое целое число Р > 1. Соответствующая позиционная система обозначений вещественных чисел называется Р-шной пози­ционной системой. Наиболее часто, кроме десятичной, ветре-

чаются двоичная и троичная системы, где Р есть соответ­ственно 2 илн 3. В двоичной системе для записи любого вещественного числа используются лишь цифры 0 н 1, а в троичной — цифры 0, 1 и 2.

6.Модуль действительного числа

1. Модуль действительного числа

и его свойства В младших классах вы уже встречались с понятием модуля (или абсолютной величины) числа, пользовались обозначением | а |. Вы знаете, что, например, | 5 | = 5, | - 3 | = 3. Правда, раньше речь шла только о рациональных числах. Теперь надо ввести понятие модуля для любого действительного числа.

Определение. Модулем неотрицательного действительного числа х называют само это число: | х | = х; модулем отрицательного действительного числа х называют противоположное число: I х | = - х.

7.Лемма Кантора о вложенных отрезках