
|
Читайте также: |
Множество натуральных чисел:
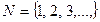 .
.
На этом множестве выполнимы операции сложения и умножения. Остальные арифметические действия могут вывести за «пределы» множества натуральных чисел. Т.е. в результате сложения и умножения мы всегда получаем натуральное число.
Поскольку на множестве 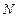 не всегда можно было произвести вычитание, возникла необходимость расширения понятия числа. Поэтому было введено множество целых чисел
не всегда можно было произвести вычитание, возникла необходимость расширения понятия числа. Поэтому было введено множество целых чисел
 .
.
На этом множестве уже выполнимы операции сложения, вычитания и умножения.
Для того, чтобы выполнялась во множестве чисел операция деления произошло расширение понятия числа до множества рациональных чисел  .
.
Рациональное число определяется как обыкновенная дробь:
 где
где 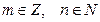 .
.
Множество рациональных чисел можно определить также как множество бесконечных периодических десятичных дробей, например,  .
.
Во множестве  определены операции сложения, вычитания, умножения, деления (кроме деления на нуль).
определены операции сложения, вычитания, умножения, деления (кроме деления на нуль).
Множество иррациональных чисел  определяется как множество бесконечных непериодических десятичных дробей. Необходимость расширения понятия числа была вызвана многими практическими задачами, например, диагональ квадрата со стороной 1 уже не выражалась рациональным числом (
определяется как множество бесконечных непериодических десятичных дробей. Необходимость расширения понятия числа была вызвана многими практическими задачами, например, диагональ квадрата со стороной 1 уже не выражалась рациональным числом ( ).
).
Объединение множеств  и
и  называется множеством действительных чисел
называется множеством действительных чисел  .
.
Между множеством всех действительных чисел и множеством точек прямой существует взаимно однозначное соответствие, т.е. каждой точке прямой соответствует единственное действительное число и наоборот (каждому действительному числу на прямой соответствует единственная точка). Такую прямую называют числовой прямой.
Во множестве  выполнимы операции сложения, вычитания, умножения, деления (кроме деления на нуль), извлечение корня с нечетным показателем.
выполнимы операции сложения, вычитания, умножения, деления (кроме деления на нуль), извлечение корня с нечетным показателем.
Однако операция извлечения корня с четным показателем из отрицательного числа на множестве  невыполнима. Снова приходим к необходимости расширения понятия числа.
невыполнима. Снова приходим к необходимости расширения понятия числа.
Условно для действительных чисел и подмножеств  можно дать следующую иллюстрацию с помощью кругов Эйлера-Вена.
можно дать следующую иллюстрацию с помощью кругов Эйлера-Вена.

 .
.
Поскольку все места на числовой прямой «заняты» действительными числами, то расширение множества действительных чисел до нового множества уже будет иметь иную геометрическую иллюстрацию – не на числовой прямой.
Для того, чтобы выполнялась операция извлечения корня с четным показателем из отрицательного числа вводят множество комплексных чисел  .
.
Дата добавления: 2014-12-15; просмотров: 54 | Поможем написать вашу работу | Нарушение авторских прав |