Читайте также:
|
Общее правило: за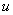 
всегда обозначается многочлен
Пример 7
Найти неопределенный интеграл.
Интегрируем по частям:
Пример 8
Найти неопределенный интеграл
Это пример для самостоятельного решения
Пример 9
Найти неопределенный интеграл
Еще один пример с дробью. Как и в двух предыдущих примерах за 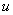обозначается многочлен.
Интегрируем по частям:
Если возникли трудности или недопонимание с нахождением интеграла 
, то рекомендуется просмотреть тему интегралы от тригонометрических функций.
Пример 10
Найти неопределенный интеграл
Это пример для самостоятельного решения.
Подсказка: перед использованием метода интегрирования по частям следует применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее.
Решения и ответы:
Пример 3: Решение:
Пример 4: Решение:
Интегрируем по частям:
Пример 6: Решение:
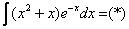
Дважды интегрируем по частям:
Пример 8: Решение:
Интегрируем по частям:
Пример 10: Решение:
Интегрируем по частям:
Примечание: Здесь мы использовали известную тригонометрическую формулу двойного угла 
. Её можно было использовать и сразу: 
, а потом интегрировать по частям.
Похожим способом также решаются интегралы вроде 
, 
– в них необходимо (сразу или в ходе решения) понизить степень синуса (косинуса) с помощью соответствующих формул. Пример 12:
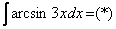
Интегрируем по частям:
Пример 13:
Интегрируем по частям:
Выполнить проверку.
Адаптированный материал www.mathprofi.ru Емелин Александр. Высшая математика просто и доступно
Дата добавления: 2015-02-22; просмотров: 50 | Поможем написать вашу работу | Нарушение авторских прав |