Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Непрерывность функции в точке.

Пусть функция у = f(x) определена в точке х ₀ и в некоторой окрестности этой точки. Функция у =f(x) называется непрерывной в точке х ₀, если существует предел функции в этой точке и он равен значению функции в этой точке, т. е.

f(x) = f(х ₀). (2.1)

Это равенство означает выполнение трех условий:

1. функция f(x) определена в точке х ₀ и в ее окрестности;

2. функция f(x) имеет предел при x ® х ₀;

3. предел функции в точке х ₀ равен значению функции в этой точке, т. е. выполняется равенство (2.1);

Так как х = х ₀, то равенство (2.1) можно записать в виде:

f(x) = f( х) = f(х ₀). (2.2)

Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функцию f(x) вместо аргумента х подставить его предельное значение х ₀.

Например, . В первом равенстве функция и предел поменялись местами (см..(2.2)) в силу непрерывности функции е ^х.

Пример. Вычислить А = .

Решение:

Отметим, что ln(1 + x) ~ x при x ® 0.

Можно дать еще одно определение непрерывности функции, опираясь на понятия приращения аргумента и функции.

Пусть функция у = f(x) определена в некотором интервале (a;b). Возьмем произвольную точку х ₀ Î(a;b). Для любого х Î (a;b) разность х - х ₀ называется приращением аргумента х в точке х ₀ и обозначается D х («дельта х»): D х = х - х ₀. Отсюда х = х ₀ + D х.

Разность соответствующих значений функций f(x) - f(х ₀) называется приращением функции f(x) в точке х ₀ и обозначается Dу (или Df или Df(х ₀)): Dу = f(x) - f(х ₀) или Dу = f(х ₀ + D х) - f(х ₀). (см. рис.2.2)

Очевидно, приращения D х и Dу могут быть как положительными, так и отрицательными числами.

Запишем равенство (2.1) в новых обозначениях. Так как условия х ® х ₀ и х - х ₀ ® 0 одинаковы, то равенство (2.1) принимает вид (f(x) - f(х ₀)) = 0 или

Dу = 0. (2.3)
Рис. 2.2

Полученное равенство (2.3) является еще одним определением непрерывности функции в точке: функция у = f(x) называется непрерывной в точке х ₀, если она определена в точке х ₀ и ее окрестности и выполняется равенство (2.3), т. е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Исследуя непрерывность функции в точке, применяют либо равенство (2.1) либо равенство (2.3).

Пример. Исследовать на непрерывность функцию у = sin x.

Решение: Функция у = sin x определена при всех x Î R.

Возьмем произвольную точку x и найдем приращение Dу:

Dу = sin (x + D x) – sin x = 2 cos (x + ) × sin .

Тогда Dу = 2 cos (x + ) × sin = 0, так как произведение ограниченной функции и бесконечно малой функции есть бесконечно малая функция.

Согласно выражению (2.3), функция у = f(х) непрерывна в точке x.

Вопрос№46

Определение 2.12 Вторым замечательным пределом называется предел

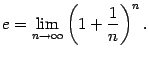
Число , заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число часто называют основанием натуральных логарифмов.

Теорема 2.15 Второй замечательный предел существует. Его значение -- число, лежащее между и .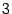

Более подробное изучение числа показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:

Определение 2.11 Первым замечательным пределом называется предел

Теорема 2.14 Первый замечательный предел равен

Доказательство. Рассмотрим два односторонних предела 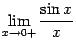и и докажем, что каждый из них равен 1. Тогда потеореме 2.1 двусторонний предел также будет равняться 1.

Вопрос №45

1. Теоремы о пределах.

Теорема. 1. Предел суммы есть сумма пределов.

Теорема. 2. Предел произведения есть произведение пределов.

Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).

Теорема. 4. Если u (x) £ z (x) £ v (x), и lim _{x ® a} u (x)=lim _{x ® a} v (x)= b, то lim _{x ® a} z (x)= b. ("Теорема о двух милиционерах").

Вопрос№44

Вопрос №43

Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1 /f(x) является бесконечно малой при x→a.

Доказательство. Возьмем произвольное число ε >0 и покажем, что при некотором δ>0 (зависящим от ε) при всех x, для которых |x – a|<δ, выполняется неравенство , а это и будет означать, что 1/f(x) – бесконечно малая функция. Действительно, так как f(x) – бесконечно большая функция при x→a, то найдется δ>0 такое, что как только |x – a|<δ, так | f(x)|> 1 / ε. Но тогда для тех же x .