Читайте также:
|
Смешанным произведением трех векторов 
называется число 
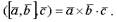
Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на этих векторах.
Пусть правая тройка векторов. Действительно, объем параллелепипеда, построенного на векторах , равен площади основания 
на высоту 
. Здесь φ - угол между векторами 
и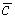 
.
Знак смешанного произведения совпадает со знаком cosφ, и поэтому смешанное произведение положительно, когда тройка векторов правая, и отрицательно, если тройка векторов левая.
Если перемножаемые векторы лежат в одной плоскости (cosφ = 0), то 
- необходимое и достаточное условие компланарности векторов.
Пусть векторы заданы своими разложениями по ортам в декартовой системе координат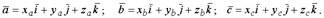 
.
Известно, что 
. Скалярно умножим этот вектор на вектор 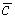и, учитывая свойства скалярного произведения, получим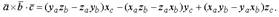 
Это выражение может быть получено при вычислении определителя 
по элементам третьей строки, исходя из правила вычисления определителя.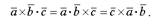 
Поэтому смешанное произведение трех векторов обозначают как , не подчеркивая при этом, какая пара векторов умножается векторно.
Дата добавления: 2015-01-30; просмотров: 21 | Поможем написать вашу работу | Нарушение авторских прав |