
Читайте также:
|
Отношение F  X × Y называется отображением X в Y или функцией, определенной в X и принимающей значения в Y, если для x:
X × Y называется отображением X в Y или функцией, определенной в X и принимающей значения в Y, если для x:
x, y1 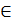 F
F  x, y2
x, y2 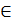 F
F  y1 = y2.
y1 = y2.
Если, x, y 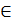 F, то элемент y называется значением F в x и обозначается как y = F x.
F, то элемент y называется значением F в x и обозначается как y = F x.
Используются также обозначения:
F: X → Y;
F: x → F x.
Принципиально важным свойством отображения является то, что любому значению "аргумента" x ставится в соответствие единственный элемент y. Такое понятие, как "многозначная" функция, здесь не рассматривается. Вполне правомерно, конечно, определить отображение, значениями которого являются подмножества некоторого данного множества, состоящие более чем из одного элемента. Но такое определение практически бесполезно, т. к. не удается разумным образом определить алгебраические операции над значениями таких функций. Например, операция извлечения корня из вещественного числа √ z приводит к двум значениям со знаками "плюс" и "минус". Но тогда как понимать равенство: √ z +√ z =2√ z? Левая часть имеет три разных значения, а правая — только два. (Хотя, конечно, существует и понятие Римановой поверхности.)
Сделаем еще одно замечание. Обычно (в "школьной" математике) различают понятия функции и ее графика. В данном выше определении эти понятия совпадают. В современной математике важнейшую роль играет рассмотрение отображения (функции) как единого объекта (такого же, как точка или число) и проведение ясного различия между отображением F и любым из его значений Fx. Первое есть элемент множества отображений X в Y, обозначаемого как  X×Y, второе — элемент множества Y, причем
X×Y, второе — элемент множества Y, причем
F = x, y 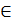 X × Y/ y =Fx.
X × Y/ y =Fx.
Таким образом, отображение F есть некоторое множество упорядоченных пар x, y.
Пусть F: X →Y. Пусть также A  X. Тогда множество
X. Тогда множество
F A = y 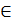 Y/
Y/  x
x 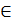 A y = F x
A y = F x
называется образом множества А при отображении F. Здесь  — квантор существования
— квантор существования  читается: существует х. Прообразом множества B
читается: существует х. Прообразом множества B  Y при отображении F называется множество
Y при отображении F называется множество
 B =
B = 
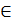 X / F
X / F 
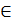 B
B
Пусть F: X →Y. Пусть A  X. Тогда множество
X. Тогда множество
F  (A × Y)
(A × Y)  A ×Y
A ×Y
называется сужением отображения F на множестве А.
Дата добавления: 2015-02-16; просмотров: 27 | Поможем написать вашу работу | Нарушение авторских прав |