Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Статистический (частотный) подход к определению вероятности.

Классическое определение вероятности Р(А) события А как отношения числа благоприятных элементарных исходов m к числу всех элементарных исходов n предполагает, что все элементарные исходы равновероятны. Однако, это условие далеко не всегда выполняется, поэтому мы сейчас введем еще одно определение вероятности - статистическое (или частотное).

Как оценить вероятность интересующего нас события, если в процессе испытания элементарные исходы вовсе не обязаны быть равновероятными? Строго говоря, необходимо было бы много раз проделать интересующий нас опыт и узнать частоту реализации различных элементарных исходов. В пределе, при увеличении числа испытаний, отношение числа m реализованных событий А к общему количеству испытаний n и будет определять вероятность Р(А)=m/n.

Важно понимать, что статистический подход не противоречит классическому, а лишь расширяет границы возможного применения аппарата теории вероятностей. Поэтому все приемы, которые Вы уже освоили в рамках классической схемы, можно будет использовать и в дальнейшем.

Для решения практических задач нам понадобятся следующие важные теоремы.

1. Теорема сложения вероятностей для несовместных событий:
P(A + B) = P(A) + P(B) - вероятность наступления в результате эксперимента хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий.

Обсуждение. Напомним, что события А и В называются несовместными, если в результате опыта они не могут появиться вместе. (Пожалуйста, не путайте их с независимыми событиями, которые мы обсуждали в прошлом разделе. Независимые события могут спокойно сосуществовать друг с другом.)

Пример. По статистике, в прошлом году 10% жителей нашего города встретили Новый год в отъезде, 40% ходили в гости или в ресторан, оставаясь в городе, остальные встречали Новый год дома. Считая, что эта тенденция сохранится, посчитайте вероятность того, что житель нашего города встретит Новый год дома.

Решение: здесь можно смело пользоваться теоремой сложения вероятностей, т.к. события встречи Нового года в разных местах одним и тем же человеком - несовместны. Поэтому все, кто встретит Новый год в гостях или в другом городе (они составят вместе 40%+10%), не смогут встретить его дома. Принимая общее число жителей города за 100%, найдем, что 50% оставалось дома в прошлый раз. Полагая, что эти же пропорции сохранятся и в этом году, найдем, что вероятность встретить Новый год дома для жителя нашего города равна Р=0,5. (Заметим, что в данном случае нам было удобно посчитать сначала вероятность обратного события, а потом вычесть результат из 100%.)

Что произойдет, с нашими оценками, если исходные события не являются несовместными? Давайте немного изменим предыдущий пример.

Пример. Владелец фирмы частных такси хочет сделать прогноз количества клиентов на новогоднюю ночь. Пусть, по его сведениям, в прошлом году Новый год встретили дома 50%, в компании друзей или родственников, но не выезжая из города - 80%, в отъезде были 10%. Почему у него получилось в сумме больше 100%?

Видимо, каких-то жителей он посчитал больше одного раза. Скорее всего, тех, кто сидел дома, но, одновременно, принимал друзей или родственников, которые пришли к нему в гости. Поскольку эти события не являются несовместными, просто складывая вероятности, он завышает свои оценки.

Впрочем, это относится не только к оценке вероятности события, но и к решению любых задач на подсчет элементов объединения двух множеств путем сложения. Если множества частично перекрываются, сумма их элементов будет больше, чем реальное количество элементов, поскольку при арифметическом сложении элементы этого "перекрытия" мы невольно посчитали дважды, и как входящие в первое множество, и как входящие во второе. Выход здесь один: мы должны заметить, что множества частично "перекрываются", посчитать число элементов в их общей части и вычесть это число из суммы (т.к. при суммировании мы его посчитали дважды).

8) Несовместные события. Теорема сложения вероятности и её обобщение.

Случайные события называются несовместными если появление одного исключает появление другого. Теорема сложения вероятностей позволяет вычислять вероятности суммы двух или нескольких событий. Для двух событий теорема формулируется следующим образом.

Вероятность суммы двух событий равна сумме вероятностей этих событий минус вероятность их произведения: P(A+B)= P(A) + P(B) – P(AB).

Докажем теорему для схемы случаев. Пусть общее число элементарных исходов равно N, причем k из них влекут за собой событие А, l исходов - событие В и m - событие АВ. Из условия и рис.1.14 следует, что вероятности событии А, В и АВ равны: P(A)= k/N, P(B)= l/N, P(AB)= m/N.

Объединению (сумме) событий А и В благоприятствует k+(l-m) событий. Следовательно,

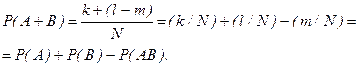
Теорему сложения вероятностей можно обобщить на случай, когда число событий больше двух. Так, например, формула для вычисления вероятности суммы трех совместных событий имеет вид

P(A+B+C)= P(A)+P(B)+

+P(C)-P(AB)-P(AC)-P(BC)+P(ABC). (1.13.2)

Справедливость этой формулы наглядно следует из геометрической интерпретации (рис.1.15).

Теорема сложения доказывается только для схемы случаев. Если ситуация к схеме случаев не сводится, то теорема обосновывается тем, что приведенные в доказательстве соотношения справедливы для относительных частот. Действительно, если при N_c испытаниях событие А появилось k_c раз, событие В - l_c раз и событие АB - m_c раз, то событие А+В осуществилось (k_c+l_c-m_c) раз. Таким образом,

P*(A+B)= (k_c+l_c-m_c)/N_c=(k_c/N_c)+(l_c/N_c)-(m_c/N_c)=

= P*(A)+P*(B)-P*(AB). (1.13.3)

Если число N_c испытаний достаточно велико, то соотношения для частот переходят в соотношения для вероятностей, а формула (3) переходит в (1).

Из теоремы сложения вытекает ряд следствий.

Следствие 1. Вероятность суммы несовместных событий А₁ и А₂ равна сумме вероятностей этих событий:

P(А₁+А₂)= P(А₁)+P(А₂). (1.13.4)

В самом деле, если А₁ и А₂ несовместны, то Р(А₁А₂)=0. Тогда из (1) следует (4).

Следствие 2. Сумма вероятностей несовместных событий, составляющих полную группу, равна единице:

(1.13.5)

Действительно, пусть события А₁, А₂,..., А_n несовместны и составляют полную группу. Тогда по теореме сложения будем иметь

P(А₁+А₂+…+А_n)=P(А₁)+P(А₂)+…P(А_n).

Так как событие А₁+А₂+…+А_n достоверно, ибо оно осуществляется при каждом опыте и вероятность его равна единице, то

Следствие 3. Сумма вероятностей противоположных событий А и равна единице:

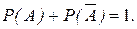(1.13.6)

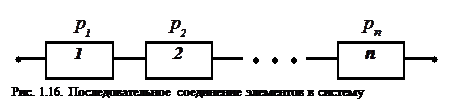
Для доказательства учтем, что А и - несовместные события, образующие полную группу. Поэтому следствие 3 является частным случаем следствия 2. Оно выделено в виду его особой важности. Часто оказывается легче вычислить вероятность противоположного события , чем прямого. Тогда сначала определяют Р (), а затем находят вероятность Р(А) по формуле

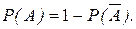(1.13.7)