Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Методы численного интегрирования Ньютона-Котеса. Линейная аппроксимация подынтегральной функции

Способ получения формул для вычисления приближенного значения интеграла в методах Ньютона-Котеса состоит в следующем. Разобьем отрезок интегрирования [ a, b ] на n частичных отрезков [ x_{i- 1}, x_i ] (i = 1, 2, ...,n, a = x ₀ < x ₁ <...< b = x_n). Введенные промежуточные точки разбиения a=x ₀ ,x ₁,... ,b=x_n называют узлами интегрирования, а расстояния между узлами h_i = x_i - x_{i- 1}– шагами интегрирования. Если шаг интегрирования постоянный (сетка равномерная), то ее шаг h = h_i = (b - a)/ n. Если на каждом частичном отрезке интегрирования [ x_{i- 1}, x_i ] аппроксимировать подынтегральную функцию интерполяционным полиномом, то для данного вида заменяющей функции j _i (x) несложно будет найти соответствующий частичный интеграл (11.17).

11.3.1.Методы прямоугольников

Простейшим видом полиномов являются константы, т.е. полиномы нулевой степени: Р ₀(x)= C. Данная замена используется в методах прямоугольников. Если подставить на каждом частичном отрезке [ x_{i- 1}, x_i ]: f (x)» j _i (x) = c_i, то формула (11.17) принимает вид:

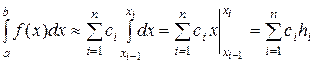. (11.18)

В формуле (11.18) точное значение определенного интеграла как площади под интегральной кривой приближенно заменяется суммой площадей прямоугольников, одна из сторон которых есть длина отрезка интегрирования h_i, а другая – аппроксимирующая константа c_i. Отсюда происходит и название методов. Заметим, что аппроксимация подынтегральной функции f (x) на частичном отрезке [ x_{i- 1}, x_i ] константой c_i неоднозначна, ее можно выбирать, исходя из различных условий.

Выбирая константу c_i,равную значению подынтегральной функции в левой (рис. 11.2 а) или правой (рис. 11.2 б) границах отрезка [ x_{i- 1}, x_i ], приходим к формулам левых и правых прямоугольников, соответственно:

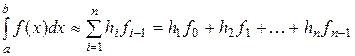, (11.19)

. (11.20)

где f_{i- 1} = f (x_{i- 1}), f_i = f (x_i) - значения f (x) в левой и правой границах отрезка [ x_{i- 1}, x_i ].

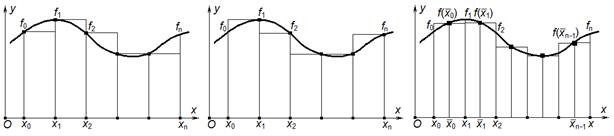
а б в

Рис. 11.2. Методы левых (а) и правых (б) прямоугольников, метод средних (в)

В случае постоянного шага интегрирования h_i = h формулы (11.19) и (11.20) приобретают вид:

, (11.21)

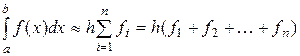. (11.22)

Наиболее широко на практике используется формула средних прямоугольников, в которой значение константы c_i (высота прямоугольника) выбирается равной значению подынтегральной функции в средней точке` x_i отрезка интегрирования (рис. 11.3):

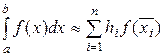, . (11.23)

В случае постоянного шага интегрирования h_i = h формула средних прямоугольников (11.23) будет иметь следующий вид:

,

где ` x_i = а + h× (i - 0,5). (11.24)

Из трех рассмотренных методов прямоугольников метод средних прямоугольников является наиболее точным.

Замечание. Если подынтегральная функция f (x) задана не аналитическим выражением, а таблицей, то формулу средних прямоугольников непосредственно применить невозможно, поскольку значения функции известны лишь в узловых точках.

11.3.2.Метод трапеций

В данном методе на частичных отрезках [ x_{i- 1}, x_i ] подынтегральную функцию f (x) заменяют интерполяционным полиномом первой степени, т.е. наклонной прямой, проходящей через точки с координатами (x_{i- 1}, f_{i- 1}) и (x_i, f_i) (рис. 11.3):

. (11.25)

Рис.11.3. Метод трапеций для постоянного шага интегрирования

Поставляя это выражение в общую формулу (11.17) и выполняя интегрирование по частичным отрезкам приходим к формуле трапеций:

. (11.26)

Название метода связано с тем, что интеграл по частичному отрезку [ x_{i- 1}, x_i ] заменяется площадью трапеции с основаниями, равными значениям функции f (x) на краях отрезка, и высотой, равной h_i = x_i+1 - x_i (рис. 11.3).

В случае постоянного шага интегрирования h формула трапеций принимает вид

. (11.27)

Также формулу (11.27) часто записывают следующим образом:

. (11.28)

Несмотря на то, что в методе трапеций используется более высокий порядок интерполяции подынтегральной функции (первый), по сравнению с методом прямоугольников, который использует интерполяцию нулевого порядка, точность метода трапеций оказывается ниже точности метода средних прямоугольников. Более высокая точность метода средних прямоугольников объясняется лучшим приближением функции за счет выбора узловых точек для ее вычисления.

Пример 1. Для функции f (x) = sin x определить приближенные значения определенного интеграла на отрезке [-p/6;p] с шагом p/6 по методам 1) левых, 2) правых, 3) средних прямоугольников, 4) трапеций и найти их абсолютную погрешность.

Решение. Первообразная функции f (x): F (x) = -cos x. Точное значение рассмотренного определенного интеграла на отрезке [-p/6;p] равно:

I _т = - (cos(p)-cos(-p/6))» - (-1 - 0,866025) = 1,866025.

Узловые точки: x ₀=-p/6; x ₁=0; x ₂=p/6; x ₃=p/3; x ₄=p/2; x ₅=2p/3; x ₆=5p/6; x ₇=p.

Узловые значения функции f (x) с точностью до 6 знака после запятой:

f ₀= -0,5; f ₁=0; f ₂=0,5; f ₃ » 0,866025; f ₄=1; f ₅» 0,866025; f ₆=0,5; f ₇ = 0.

Приближенные значения интеграла по методам 1,2 и 4:

1) левых прямоугольников:

S₁ = (p/6)×(-0,5 + 0 + 0,5 + 0,866025 + 1 + 0,866025 + 0,5)» 1,692297,

2) правых прямоугольников:

S₂=(p/6)×(0+0,5+0,866025+1+0,866025+0,5+0)» 1,954097.

4) трапеций:S₄=(p/6)×(-0,5/2+0+0,5+0,866025+1+0,866025+0,5+0/2)» 1,823197.

Значения функции f (x) в средних точках между узлами:

f _0с= sin(-p/12)= -0,258819; f _1с = sin(p/12)= 0,258819; f _2с = sin(p/4)= 0,707107;

f _3с = sin(5p/12)= 0,965926; f _4с = sin(7p/12)= 0,965926; f _5с = sin(3p/4)= 0,707107;

f _6с = sin(11p/12)= 0,258819.

Приближенное значения интеграла по методу средних прямоугольников:

S₃ = (p/6)×(f _0с + f _1с + f _2с + f _3с + f _4с + f _5с + f _6с)» 1,887513.

Абсолютные погрешности значений D _i = ½S_i - I _т½:

D₁ = 0,173728; D₂ = 0,088072; D₃ = 0,021488; D₄ = 0,042828.

Вопросы для проверки знаний.

1. Какой вид аппроксимации подынтегральной функции используется в методах Ньютона-Котеса?

2. Каким видом полиномов заменяют подынтегральную функцию в методах прямоугольников?

3. Какой вид полиномов применяется для аппроксимации подынтегральной функции в методе трапеций?

4. Какой из способов линейной аппроксимации подынтегральной функции при численном интегрировании дает наибольшую точность?