Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ (НАПРЯЖЕНИЙ)

Метод узловых потенциалов, как и метод контурных токов, требует совместного решения меньшего числа независимых уравнений по сравнению с методом узловых и контурных уравнений (применением двух законов Кирхгофа), что сокращает расчеты. Он основан на применении первого закона Кирхгофа.

Для расчета токов методом узловых потенциалов, кроме первого закона Кирхгофа, применяется обобщенный закон Ома. Рассмотрим его применение для отдельных ветвей, представленных на рис. 2.25,а и б. Сопротивления r₁

Рис. 2.25 К обобщенному закону Ома

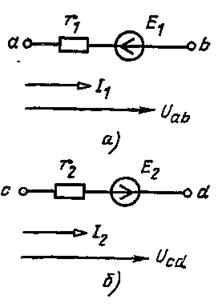
Рис 2.26. Схема к примеру 2.9

и r₂ — это суммарные сопротивления элементов каждой из ветвей ЭДС в общем случае могут быть суммами ЭДС в каждой из ветвей. Для токов указаны выбранные положительные направления.

По тем же правилам, что и в § 1.14, запишем потенциалы точек a и с:

и определим токи через разности потенциалов:

(2.46а)

(2.46б)

Эти зависимости токов от напряжения между выводами ветви и ее параметрами и называются обобщенным законом Ома. Потенциал вывода, от которого ток оттекает, входит в (2.46) со знаком “+”, а потенциал вывода, к которому ток притекает, — со знаком “-”. Со знаком “+” записывается ЭДС, направление которой совпадает с положительным направлением тока (E₂), и со знаком «-» направленная навстречу (Ε₁).

Расчет токов методом узловых потенциалов рассмотрим на примере цепи рис. 2.24 с тремя узлами А, Б, В.

Для двух узлов можно составить независимую систему уравнений по первому закону Кирхгофа. Например, для узлов А и Б

I₁-I₄ – I₃= 0 -I₁ + I₄ + I₅-I₂ = 0. (2.47)

Токн I₁ и I₂ запишем по обобщенному закону Ома (2.46).

а остальные токи по закону Ома:

Как указывалось (§ 1.14), потенциал одной из точек цепи можно принять равным нулю. Выберем, например, равным нулю потенциал узла В и подставим выражения для токов в уравнения (2.47).

Для узла А

Для узла Б

Заменим сопротивления ветвей проводимости g=I/r и перенесем слагаемые с ЭДС в правую часть уравнений. Получим для узла А

(g₁ + g₂ + g₃) φ _А – (g₁ + g₄)φ_Б = – g₁ Е₁ (2.48а) и для узла Б

- (g₁ + g₄)φ _А + (g₁ + g₄ + g₅ + g₂) φ_Β =g₂ E₂ (2.48б)

Из полученной системы уравнений после совместного решения определяются неизвестные величины, а именно потенциалы узлов φ_А и φ_Б.

Сумма проводимостей ветвей, присоединенных к узлу, называется собственной узловой проводим остью, например g_A = g₁+g₄+g₃, так как к узлу А присоединены 1-я, 4-я и 3-я ветви. Сумма проводимостей ветвей, соединяющих два узла, называется общей узловой проводимостью, например, g_AБ = g₁+g₄.

Метод узлового напряжения (§ 2.9) является частным случаем метода узловых потенциалов для цепи с двумя узлами.

Систему уравнений (2.48) можно составить и сразу, учитывая, что в (2.48) собственная проводимость входит со знаком «+», а перед общей проводимостью стоит знак «—». В правой части в общем случае записываются алгебраические суммы произведений gE: со знаком «+» для ЭДС, направленных к узлу, для которого составляется уравнение, и со знаком «—» для ЭДС, направленных от узла. Таким образам, в общем случае (цепь с числом узлов более трех), например, для узла А

(2.49)

Таким образом, уравнение для данного узла содержит произведение потенциала узла на сумму проводимостей всех ветвей, присоединенных к этому узлу, и произведения потенциалов других узлов на общие проводимости.

Если схема электрической цепи содержит источник тока, подключенный к узлу А, то в правой части (2.49) дополнительно записывается ток I_к со знаком «+», если он направлен к узлу, и со знаком «—» в противном случае.

Аналогично (2.49) надо составить уравнения для всех других узлов, кроме одного, потенциал которого принят равным нулю.

Из сравнения методов узловых и контурных уравнений, контурных токов и узловых потенциалов следует, что для определения токов в цепи первый метод требует совестного решения большего числа уравнений (равного числу ветвей с неизвестными токами). Методом контурных токов составляется и решается совместно только число уравнении, равное числу контурных уравнений, а методом узловых потенциалов – число уравнений, равное числу узловых уравнений.

Пример 2.9. Методом узловых потенциалов определить токи в цепи рис 2.26 с параметрами r₁=2 Ом, г₂= 10 Ом, r₃=r₅=4 Ом, г_вт4=1 Ом, r₄=3 Ом, Ε’₁ =2 В, E”₁ =20 В, Е₄=4 В, E₅=6 В. На рис. 2.26 показано, что заземлена точка В, т. е. принято φ_в=0.

Решение Для цепи с тремя узлами нужно составить два узловых уравнения (по первому закону Кирхгофа), например для узлов А и В.

Выберем положительные направления токов, показанные на рис. 2.26. Для узла А

Для узла Б

Каждый из токов запишем по обобщенному закону Ома (2.46) или по закону Ома:

Подставим эти значения токов в узловые уравнения:

или

Из полученных двух уравнений находим неизвестные потенциалы:

φ_Α = 10 В, φ_Б =6 В.

Последнюю систему уравнений можно составить сразу по типу (2.29). Например в 1-м уравнении

g_А=g₁+g₂+g₃+g₄=0,5+0,1+0,25+0,25 См —это сумма проводимостей ветвей, присоединенных к узлу А,

g_AБ =g₃ + g₄=0,25+0,25 Cm—сумма проводимостей ветвей, соединяющих узлы А и Б;

правая часть уравнения.

Аналогично для узла Б проводимость

Для цепей с большим числом контуров и узлов необходимо решать совместно систему многих уравнений. Поэтому следует проводить расчеты на ЭВМ.

9.Преобразование звезды в треугольник и треугольника в звезду. Соединение трех сопротивлений, имеющее вид трехлучевой звезды (рис. 2.25), называют звездой, а соединение трех сопротивлений так, что они образуют собой стороны треугольника (рис. 2.26), — треугольником. В узлах 1, 2, 3 (потенциалы их Φ₁, Φ₂ и Φ₃) треугольник и звезда соединяются с остальной частью схемы (не показанной на рисунках).
Обозначим токи, подтекающие к узлам 1, 2, 3, через I₁, I₂ и I₃.
Часто при подсчете электрических цепей оказывается полезным преобразовать треугольник в звезду или, наоборот, звезду в треугольник. Практически чаще бывает необходимо преобразовывать треугольник в звезду. Если преобразование выполнить таким образом, что при одинаковых значениях потенциалов одноименных точек треугольника и звезды подтекающие к этим точкам токи одинаковы, то вся внешняя схема «не заметит» произведенной замены. Выведем формулы преобразований. С этой целью выразим токи I₁, I₂ и I₃3 в звезде и в треугольнике через разности потенциалов точек и соответствующие проводимости.
Для звезды

Подставим (2.24) в (2.23) и найдем Φ₀:

откуда

Введм Φ₀ в выражение (2.24) для тока I ₁:

Для треугольника в соответствии с обозначениями на рис. 2.26

Так как ток I ₁, в схеме рис. 2.25 равен току I ₁ в схеме рис. 2.26 при любых значениях потенциалов Φ₁Φ₂Φ₃, то коэффициент при Φ₂ в правой части (2.27) равен коэффициенту при Φ₂ в правой части (2.26), а коэффициент при Φ₃ в правой части (2.27) — коэффициенту при Φ₃ в правой части (2.26).
Следовательно

Аналогично,

Формулы (2.28) — (2.30) дают возможность определить проводимости сторон треугольника через проводимости лучей звезды. Они имеют легко запоминающуюся структуру: индексы у проводимостей в числителе правой части соответствуют индексам у проводимости в левой части; в знаменателе — сумма проводимостей лучей звезды.

Из уравнений (2.28) — (2.30) выразим сопротивления лучей звезды через сопротивления сторон треугольника:
С этой целью запишем дроби, обратыне (2.28)-(2.30):

где

Подставив (2.31),(2.33) и (2.34) в (2.32), получим

следовательно,

Подставив m в (2.33), найдем

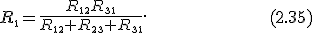
Аналогично,

Структура формул (2.35) — (2.37) аналогична структуре формул (2.28) — (2.30).
Преобразование треугольника в звезду можно пояснить, рас-смотрев, например, схему рис. 2.27, а, б. На рис. 2.27, а изображена схема до преобразования, пунктиром обведен преобразуемый треугольник. На рис. 2.27, б представлена та же схема после преобра-зования. Расчет токов произвести для нее проще (например, методом двух узлов), чем для схемы рис. 2.27, а.
В полезности преобразования звезды в треугольник можно убедиться на примере схем рис. 2.27, в, г. На рис. 2.27, в изображена схема до преобразования, пунктиром обведена преобразуемая в треугольник звезда. На рис. 2.27, г представлена схема после преобразования, которая свелась к последовательному соединению сопротивлений¹.

Пример 24. Найти значение сопротивлений R₁,R₂,R₃ в схеме рис. 2.27, б, если сопротивления R₁₂, R₁₃, R₁₃ в схеме рис. 2.27, a равны соответственно 2,3,5 Ом.
Решение По формуле (2.35),

Соединение элементов электрической цепи по схемам «звезда» и «треугольник»

В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R ₁₂, R ₁₃, R ₂₄, R ₃₄ включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.

Рис. 1.12

Рис. 1.13

В мостовой схеме сопротивления R ₁₃, R ₁₂, R ₂₃ и R ₂₄, R ₃₄, R ₂₃ соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R ₂₄ R ₃₄ R ₂₃ звездой R ₂ R ₃ R ₄ (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:

(1.8)

; ; .

Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:

(1.9)

; ; .

После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)

.

10. Нелинейные цепи

Нелинейными называются цепи, в состав которых входит хотя бы один нелинейный элемент.

Нелинейными называются элементы, параметры которых зависят от величины и (или) направления связанных с этими элементами переменных (напряжения, тока, магнитного потока, заряда, температуры, светового потока и др.). Нелинейные элементы описываются нелинейными характеристиками, которые не имеют строгого аналитического выражения, определяются экспериментально и задаются таблично или графиками.

Нелинейные элементы можно разделить на двух – и многополюсные. Последние содержат три (различные полупроводниковые и электронные триоды) и более (магнитные усилители, многообмоточные трансформаторы, тетроды, пентоды и др.) полюсов, с помощью которых они подсоединяются к электрической цепи. Характерной особенностью многополюсных элементов является то, что в общем случае их свойства определяются семейством характеристик, представляющих зависимости выходных характеристик от входных переменных и наоборот: входные характеристики строят для ряда фиксированных значений одного из выходных параметров, выходные – для ряда фиксированных значений одного из входных.

По другому признаку классификации нелинейные элементы можно разделить на инерционные и безынерционные. Инерционными называются элементы, характеристики которых зависят от скорости изменения переменных. Для таких элементов статические характеристики, определяющие зависимость между действующими значениями переменных, отличаются от динамических характеристик, устанавливающих взаимосвязь между мгновенными значениями переменных. Безынерционными называются элементы, характеристики которых не зависят от скорости изменения переменных. Для таких элементов статические и динамические характеристики совпадают.

Понятия инерционных и безынерционных элементов относительны: элемент может рассматриваться как безынерционный в допустимом (ограниченном сверху) диапазоне частот, при выходе за пределы которого он переходит в разряд инерционных.

В зависимости от вида характеристик различают нелинейные элементы с симметричными и несимметричными характеристиками. Симметричной называется характеристика, не зависящая от направления определяющих ее величин, т.е. имеющая симметрию относительно начала системы координат: 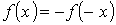. Для несимметричной характеристики это условие не выполняется, т.е. . Наличие у нелинейного элемента симметричной характеристики позволяет в целом ряде случаев упростить анализ схемы, осуществляя его в пределах одного квадранта.

По типу характеристики можно также разделить все нелинейные элементы на элементы с однозначной и неоднозначной характеристиками. Однозначной называется характеристика , у которой каждому значению х соответствует единственное значение y и наоборот. В случае неоднозначной характеристики каким-то значениям х может соответствовать два или более значения y или наоборот. У нелинейных резисторов неоднозначность характеристики обычно связана с наличием падающего участка, для которого , а у нелинейных индуктивных и емкостных элементов – с гистерезисом.

Наконец, все нелинейные элементы можно разделить на управляемые и неуправляемые. В отличие от неуправляемых управляемые нелинейные элементы (обычно трех- и многополюсники) содержат управляющие каналы, изменяя напряжение, ток, световой поток и др. в которых, изменяют их основные характеристики: вольт-амперную, вебер-амперную или кулон-вольтную.