
Читайте также:
|
Распределение Пуассона
Определение 4. Случайная величина Х имеет распределение Пуассона с параметром l, если  , m = 0, 1, …
, m = 0, 1, …
Покажем, что Σpm = 1.  .
.
Биномиальное распределение
Определение 5. Случайная величина X имеет биномиальное распределение, если  , m = 0, 1, …, n,
, m = 0, 1, …, n,
где n – число испытаний по схеме Бернулли, m – число успехов, р – вероятность успеха в единичном исходе, q = 1–p.
Гипергеометрическое распределение
Определение 2. Случайная величина Х, принимающая целочисленные значения, имеет гипергеометрическое распределение, если  , m = 0, 1, …, min (n, M). Можно показать, что
, m = 0, 1, …, min (n, M). Можно показать, что  .
.
Геометрическое распределение
Определение 3. Случайная величина X имеет геометрическое распределение, если
P (Х = m) = Pm= qm-1p, m = 1, …
где q = 1–p, p Î(0, 1). Геометрическое распределение имеет случайная величина X, равная числу испытаний по схеме Бернулли до первого наступления успеха с вероятностью успеха в единичном испытании р. Покажем, что Σ p i = 1
 .
.
Мат ожидание
Основной наиболее употребляемой характеристикой центральной тенденции является математическое ожидание МХ случайной величины.
Определений 1. Пусть Х – дискретная случайная величина,  ,
, 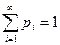 , тогда
, тогда
 , (1)
, (1)
если ряд сходится абсолютно.
Определений 2. Пусть Х – непрерывная случайная величина, p(x) – плотность распределения, тогда
 , (2)
, (2)
если интеграл сходится абсолютно.
Найдем математические ожидания случайных величин некоторых известных законов распределения.
1. Пусть Х имеет пуассоновское распределениес параметром l.
 , l>0, m = 0, 1, 2,…
, l>0, m = 0, 1, 2,…
По формуле (1) имеем  . Следовательно,
. Следовательно,
МХ = l. (3)
2. Пусть Х имеет экспоненциальное распределение с параметром l,
 .
.
По формуле (2) имеем
 .
.
Следовательно
МХ =  . (4)
. (4)
Пусть Х имеет равномерное распределение на интервале [ a,b ]
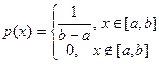 .
.
Тогда по формуле (2) имеем

Следовательно
МХ =  .
.
MX = 1 c = c.
2. M (сX) = сMX.
Это свойство следует из теорем 1, 2.
3. Если определены MX и MY, то
M (X + Y) = MX + MY,
Если Х и Y независимы, то M (X Y) = MX MY
Дисперсией случайной величины X называют число, равное математическому ожиданию квадрата отклонения случайной величины от её математического ожидания:
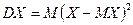 . (1)
. (1)
Если Х – непрерывная, то  . (2)
. (2)
Если Х – дискретная, то 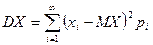 .
.
Дата добавления: 2015-04-26; просмотров: 8 | Поможем написать вашу работу | Нарушение авторских прав |