Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Комплексные числа и векторы

Существует и другой способ геометрической интерпретации комплексных чисел. Каждой точке (x, y) координатной плоскости, изображающей комплексное число
z = x + yi, соответствует единственный вектор, отложенный от начала системы координат и обратно (рис. 5). При этом двум различным точкам координатной плоскости будут соответствовать два таких различных вектора.

Таким образом, может быть установлено взаимно однозначное соответствие между множеством точек координатной плоскости (комплексными числами) и множеством векторов, отложенных от начала системы координат.

Если z = x + yi (рис. 5), то вектор , отложенный от начала системы координат до точки, изображающей число z, будет иметь координаты (x; y). Известно, что равные векторы имеют равные координаты.

Итак, мы рассмотрели два способа интерпретации комплексных чисел: их можно изображать либо точками координатной плоскости, либо векторами, отложенными от начала системы координат. При этом любые два равных вектора (имеющих одно и то же направление и равные длины) изображают одно и то же комплексное число, а векторы, отличные либо длиной, либо направлением, изображают разные числа. На рисунке 6 с помощью векторов изображены различные комплексные числа: изображает число 2 + 0i; – число – 3 + 0i; – число 0 + i; – число 0 + 2i; – число 0 – 3i; – число 3 + 2i; – число – 1 – 2i.

Ясно, что любой ненулевой вектор, лежащий на оси Oy (или параллельный ей), изображает чисто мнимое число yi, причем y > 0, если направление вектора совпадает с направлением оси, y < 0, если направление вектора противоположно направлению оси. Вследствие этого ось Oy называют мнимой. Все векторы, лежащие на оси Ox (или параллельные ей) изображают действительные числа, поэтому ее называют действительной осью.

Векторная интерпретация комплексных чисел позволяет уяснить геометрический смысл операций над комплексными числами. Например, сумма двух комплексных чисел 2 + i и 1 + 4i равна 3 + 5i. Каждое из слагаемых изображает соответствующий вектор, отложенный от начала O координат (рис. 7):

= 2 + i; = 1 + 4i.

Сумма этих векторов – вектор = 3 + 5i, изображается диагональю параллелограмма, построенного на векторах и.

Для того, чтобы лучше уяснить себе геометрический смысл умножения двух комплексных чисел, воспользуемся их тригонометрической формой. Пусть векторы изображают соответственно комплексные числа:

соответственно модули этих чисел, а j₁ и j₂ – их аргументы. Найдем произведение этих чисел:

z₁z₂ = r₁r₂(cosj₁ + i sin j₁)(cos j₂ + i sin j₂) = r₁r₂(cos j₁cos j₂ – sin j₁ sin j₂) + i = (cos j₁sin j₂ + sin j₁cos j₂).

Воспользуемся известными из школы теоремами сложения синуса и косинуса:

cos j₁cos j₂ – sin j₁ sin j₂ = cos(j₁ + j₂);

cos j₁sin j₂ + sin j₁cos j₂ = sin(j₁ + j₂).

Тогда произведение данных комплексных чисел равно комплексному числу:

z₁z₂ = r₁r₂(cos(j₁ + j₂) + isin(j₁ + j₂)).

Последнее соотношение позволяет сформулировать правило умножения комплексных чисел: при умножении двух комплексных чисел их модули перемножаются, а их аргументы складываются. Это проиллюстрировано на рисунке 8.

Ясно, что произведение комплексных чисел связано с поворотом (вращением). Так, произведение z₁z₂ изображается вектором представляющим собой образ вектора , повернутого на угол j₂ (или образ вектора , повернутого на угол j₁), при этом модуль вектора равен произведению модулей данных векторов.

Связь произведения комплексных чисел с вращением становится более наглядной, если рассматривать произведение различных комплексных чисел (векторов) на комплексное число i, у которого модуль равен 1, а аргумент 90°. Например, найдем произведение комплексных чисел z₁ = 1 + i и z₂ = i.

z = z₁z₂ = (1 + i)i = i + i² = – 1 + i.

Числа z₁ и z₂ соответственно изображают векторы и (рис.9). Мы видим, что модуль комплексного числа z равен модулю числа z₁:

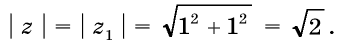
Аргумент же комплексного числа z равен 45° + 90° = 135°, в то время, как аргумент комплексного числа z₁ равен 45°. Т.е. вектор, изображающий число z, есть образ вектора, изображающего число z₁ при повороте на 90°.