Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Формула перехода от одного основания логарифма к другому

№1

Показательная функция.
Функция вида y = ax, в которой a - положительное (постоянное) число, называют показательной функцией. Аргумент x принимает любые действительные значения; значениями функции обычно рассматривают только положительные числа, потому что иначе мы получаем многозначную функцию. Например, функция y = 81 x имеет при x = 1/4 четыре различных значения: y = 3, y = -3, y = 3 i и y = -3 i. (Корень 4ой степени из 81, где i² = -1)
Так как значениями функции обычно рассматривают только положительные числа, рассматриваем в качестве значения только y = 3 1. При a >1 показательная функция возрастает, a при 0 < a < 1 – убывает.

свойства показательной функции:

- область определения функции: - бесконечночть < x < + бесконечночть (т.e. x принадлежит R);

область значений: y > 0;

- функция монотонна: возрастает при a > 1 и убывает при 0 < a < 1;

- функция неограниченная, всюду непрерывная, непериодическая;

- нулей функция не имеет.

№2

Логарифм положительного числа по основанию — это показатель степени, в которую надо возвести , чтобы получить . b > 0, a > 0, а≠ 1.

свойства логарифмов:

(, , , ,

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

Десятичный логарифм — логарифм по основанию 10. Другими словами, десятичный логарифм числа 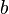есть решение уравнения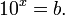

Десятичный логарифм числа 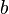существует, если

Примеры:

Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), log _e (x) или иногда просто log(x).Натуральный логарифм числа x — это показатель степени, в которую нужно возвести число e, чтобы получить x. Натуральный логарифм самого числа e равен 1, потому что e ¹ = e, а натуральный логарифм 1 равен 0, поскольку e ⁰ = 1.

Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/ x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже.

Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:

№3

Функция y = log_a х (где а > 0, а = 1) называется логарифмической.

Свойства функции у = log_aх, a > 1:

1. D(f) = (0; + );
2. не является ни четной, ни нечетной;
3. возрастает на (0; + );
4. не ограничена сверху, не ограничена снизу;
5. не имеет ни наибольшего, ни наименьшего значений;
6. непрерывна;
7. E(f) = (- ;+ );
8. выпукла вверх;
9. дифференцируема.

Свойства функции у = l og_aх, 0 < a < 1:

1. D(f) = (0;+ );
2. не является ни четной, ни нечетной;
3. убывает на (0; + );
4. не ограничена сверху, не ограничена снизу;
5. нет ни наибольшего, ни наименьшего значений;
6. непрерывна;
7. E(f) = (-; + );
8. выпукла вниз;
9. дифференцируема.

Свойства функции у = ln х:

1. D(f) = (0; + );
2. не является ни четной, ни нечетной;
3. возрастает на {0; + );
4. не ограничена сверху, не ограничена снизу;
5. не имеет ни наибольшего, ни наименьшего значений;
6. непрерывна;
7. E(f) = (- ;+ );
8. выпукла вверх;
9. дифференцируема.

№4

Формула перехода от одного основания логарифма к другому

Переход к логарифмам с новым основанием осуществляется по правилу, которое можно выразить так: логарифм числа по старому основанию равен логарифму того же числа по новому основанию, деленному на логарифм старого основания по новому основанию: .

Для доказательства этой формулы перепишем ее так: . А теперь рассмотрим выражение . Преобразуем его: . И поскольку равны значения одной и той же показательной функции, то равны и значения аргумента: .

№ 5

Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.

Единичной окружностью называют окружность радиуса 1.

№21

а) Область определения: D (cos x) = R.

б) Множество значений: E (cos x) = [ – 1, 1 ].

в) Четность, нечетность: функция четная.

г ) Периодичность: функция периодическая с основным периодом T = 2 .

д) Нули функции: cos x = 0 при x = + n, n Z.

е) Промежутки знакопостоянства:

;
.

. ж) Промежутки монотонности:

;

.

з) Экстремумы:

; .

График функции y = cos x изображен на рисунке.

№22

а) Область определения: D (tg x) = R \ { /2 + n (n Z) }.

б) Множество значений: E (tg x) = R.

в) Четность, нечетность: функция нечетная.

г ) Периодичность: функция периодическая с основным периодом T = .

д) Нули функции: tg x = 0 при x = n, n Z.

е) Промежутки знакопостоянства:

; .

ж) Промежутки монотонности: функция возрастает на каждом интервале, целиком принадлежащем ее области определения.

з) Экстремумы: нет.

График функции y = tg x изображен на рисунке.

№23

Производная, её геометрический и механический смысл

Производная степенной функции

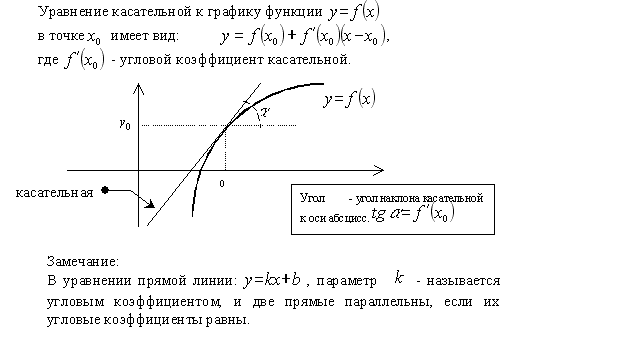
Если f(x) = xp, где p - действительное число, то Если показатель степени является отрицательным числом, т.е. f(x) = x−p, то №24 Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке. Рассмотрим график функции y = f (x): Из рис.1 видно, что для любых двух точек A и B графика функции: xf (x 0+ x)− f (x 0)= tg , где - угол наклона секущей AB. Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. Уравнение касательной Производной функции f (x) в точке x 0 называется предел отношения приращения функции в этой точке f = f (x 0+ x)− f (x 0) к приращению аргумента x при x 0: f (x 0)= lim x 0 xf (x 0+ x)− f (x 0). Геометрический смысл производной Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке.   №25 Правила дифференцирования Если функции f и g дифференцируемы в точке x 0 то в этой же точке дифференцируемы сумма, произведение и частное (если g (x 0) =0) этих функций, причем (f + g) = f + g (f g) = f g + f g (fg) = g 2 f g − f g Постоянный множитель C можно выносить из-под знака производной: (Cf) ' = Cf'. В частности, С'=0 Если f дифференцируема, то fn где n N также дифференцируема, причем (fn) = nfn −1 f Если функция y = f (x) непрерывна и строго возрастает в окрестности точки x 0 причем f (x 0) =0, то функция x = (y), обратная к функции y = f (x), дифференцируема в точке y 0 = f (x 0), причем (x 0)=1 f (x 0). Если функции y = f (x) и z = g (y) дифференцируемы в точках x 0 и y 0 = f (x 0) соответственно, то сложная функция z = g (f (x)) дифференцируема в точке x 0, причем z (x 0)= g (y 0) f (x 0). Дифференциал функции y = f (x) имеет один и тот же вид dy = f (x) dx как в случае, когда x – независимая переменная, так и в случае, когда x – дифференцируемая функция другого переменного. Если f (x) – четная функция, то f (x) – нечетная; если f (x) – нечетная функция, то f (x) – четная. Пусть в окрестности точки t 0 определены функции x (t) и y (t), причем x (t) непрерывна и строго монотонна. Пусть в этой окрестности существуют производные x (t 0) =0 и y (t 0) Тогда сложная функция y = y (t (x)), где t (x) – функция, обратная x (t), дифференцируема по x, причем dxdy = x (t) y (t). Производная Ключевые слова: функция, производная, правила нахождения производной, сложная функция Производная — основное понятие дифференциального исчесления, характеризующее скорость изменения функции. Производная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. Процесс вычисления производной называется дифференцированием. Основные правила дифференцирования: · Если функция константа, т.е. y = C, где C - число, то (С) =0. · Если функции u и v дифференцируемы в точке x, то (v + u) = v + u . · Если функция Cu, где C - постоянная, дифференцируема в точке x, то (С u) =С u . · Если функции u и v дифференцируемы в точке x, то (u v) = u v + u v . · Если функции u и v дифференцируемы в точке x и v (x) =0, то (vu) = v 2 u v − u v . Дифференцирование сложной функции. Рассмотрим функцию y = sin x2. Чтобы найти значение этой функции в фиксированнной точке x нужно: 1) вычислить x2; 2) найти значение синуса от полученного значения x2. Иными словами, сначала надо найти значение g (x) = x2, а потом найти sin g (x). В подобных случаях говорят, что задана сложная функция y = f (g (x)). В нашем примере u = g (x) = x2, а y = f (u) = sin u. Пусть y = f (g (x)) - сложная функция, причем функция u = g (x) дифференцируема в точке x, а функция y = f (u) дифференцируема в соответствующей точке u. Тогда функция y = f (g (x)) дифференцируема в точке x, причем y = f (g (x)) g (x). Запись f '(g (x)) означает, что производная вычисляется по формуле для f '(x), но вместо x подставляется g (x). Функция y=tgx 1) y= tg x, x /2, k e z y/=(tg x)/=(sin x)/(cos x)= ((sin x)/cos x- sin x(cos x)/)/cos2x= 1/cos2x;=>(tg x)/=1/cos2x