Читайте также:
|
Совокупность равенств вида 
называется системой линейных алгебраических уравнений. Здесь числа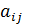 
называются коэффициентами при неизвестных, числа 
– свободные члены, а величины 
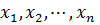- неизвестные системы. Решить систему, значит найти упорядоченную совокупность значений 
при подстановке которых в систему каждое из уравнений оказывается верным равенством. Система, имеющая хотя бы одно решение, называется совместной. Если система не имеет решений, она называется несовместной.
Различают квадратные и прямоугольные системы линейных алгебраических уравнений. Система, в которой число уравнений равно числу неизвестных называется квадратной. Если число уравнений в системе отличается от числа неизвестных, система называется прямоугольной.
Систему вида (1) можно представить в матричной форме. Для этого составим матрицу из коэффициентов при неизвестных 
.
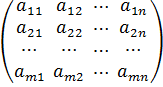Эта матрица называется основной матрицей системы. Матрицы
и 
называются соответственно: матрица – столбец неизвестных и матрица – столбец свободных членов. Таким образом, система (1) в матричной форме имеет вид: 
или в развернутом виде:
.
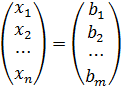Для работы с системами линейных алгебраических уравнений имеет смысл составить еще одну матрицу вида:
Такую матрицу называют расширенной матрицей системы.
Важными, для решения систем линейных алгебраических уравнений, являются определенные действия с уравнениями системы, которые не меняют решений системы. Эти действия называются элементарными преобразования систем. К числу элементарных преобразований относятся:
1. Замена строк местами.
2. Умножение любой строки на число отличное от нуля.
3. Сложение двух строк.
Перед началом решения системы линейных алгебраических уравнений целесообразно исследовать ее на совместность и определить число решений системы.
С этой целью используют теорему Кронекера – Капели. Эту теорему в данном пособии мы не приводим в связи с тем, что для ее формулировки необходимы дополнительные понятия, которые ранее в пособии не изложены. Однако приведем способ действий и правила, которые следуют из теоремы Кронекера – Капели и позволяют исследовать системы линейных алгебраических уравнений на совместность.
Исследование системы (1) на совместность начнем с того, что составим расширенную матрицу системы:
.
Расширенная матрица содержит внутри себя основную матрицу системы. Поэтому, пользуясь расширенной матрицей, мы одновременно работаем и с основной. С помощью элементарных преобразований приведем расширенную матрицу к трапециевидной форме. Для этого последовательно обнулим все элементы расположенные ниже главной диагонали. Получим матрицу одного из трех видов:
1. 
;
2. 
, (
;
3. 
.
Эти три случая показывают условия совместности и число решений системы линейных алгебраических уравнений. Охарактеризуем их.
В первом случае после преобразования к трапециевидной форме, и в основной и в расширенной матрице осталось одинаковое число ненулевых строк. Это означает то, что система является совместной. Причем, число ненулевых строк равно числу неизвестных в системе. А это значит, что система имеет единственное решение.
Во втором случае мы вновь видим то, что число ненулевых строк основной матрицы равно числу ненулевых строк расширенной матрицы. Следовательно, система является совместной. Но поскольку число ненулевых строк, оставшихся в матрице меньше числа неизвестных системы, делаем вывод, что система имеет множество решений.
В третьем случае, число ненулевых строк основной матрицы не равно числу ненулевых строк расширенной матрицы. Это означает, что система является несовместной.
Например, исследуем на совместность систему: 
Составим расширенную матрицу системы и с помощью элементарных преобразований приведем к трапециевидной форме. Расширенная матрица имеет вид:
.
Заменим местами первую и третью строки
.
Ко второй строке добавим первую строку, умноженную на 
, а к третьей строке добавим первую строку, умноженную на 
Получим матрицу:
.
Заменим местами вторую и третью строки
.
К третьей строке добавим вторую, умноженную на 7, получим:
.
Расширенная матрица приведена к трапециевидной форме. Причем, основная и расширенная матрицы содержат по три ненулевые строки. Следовательно, данная система является совместной. Число неизвестных в системе тоже равно трем. Мы получили случай совместной системы, имеющей единственное решение.
Таким образом, мы описали способ исследования системы на совместность. Теперь приведем методы решения систем линейных алгебраических уравнений.
Дата добавления: 2015-04-20; просмотров: 20 | Поможем написать вашу работу | Нарушение авторских прав |