Читайте также:
|
Среди методов решения систем линейных алгебраических уравнений наиболее часто используют три метода: метод Гаусса, метод Крамера и матричный метод. Рассмотрим каждый из них.
1. Метод Гаусса состоит в последовательном исключении неизвестных из уравнений системы. Это осуществляется с помощью приведения расширенной матрицы системы к трапециевидной форме с использованием элементарных преобразований. Само построение трапециевидной формы расширенной матрицы называется прямым ходом метода Гаусса.
В результате выполнения прямого хода метода Гаусса возникает возможность сразу исследовать систему на совместность. Практически прямой ход метода Гаусса и исследование системы на совместность это одно и тоже.
Далее, в случае совместности системы, выполняется обратный ход метода Гаусса. Неизвестные находим, использую трапециевидную расширенную матрицу. Начиная с нижней строки, выражаем все неизвестные в обратном порядке. Так, выполним обратный ход для системы
Используем уже преобразованную к трапециевидной форме, расширенную матрицу системы:
.
Из последней строки находим:
Например, решим систему 
методом Гаусса. Составим расширенную матрицу: 
.
С помощью элементарных преобразований сведем ее к трапециевидной форме. Сначала поменяем местами первую и третью строки 
.
Добавим ко второй строке первую строку, умноженную на 
К третьей строке добавим первую строку, умноженную на 
. И к четвертой строке добавим первую строку, умноженную на .
Получим: 
.
Разделим третью строку на 5 и поменяем ее местами со второй строкой 
.
К третьей строке добавим вторую строку, умноженную на , а к четвертой строке добавим вторую строку, умноженную на 
.
Третью строку умножим на
К четвертой строке добавим третью строку, умноженную на 2 
.
Разделим четвертую строку на 
. В итоге таких элементарных преобразований мы свели расширенную матрицу системы к трапециевидной форме 
Таким образом, мы выполнили прямой ход метода Гаусса и кроме этого, можем провести исследование исходной системы на совместность. Так система совместна (число ненулевых строк основной и расширенной матриц одинаково и равно четырем) и имеет единственное решение (число ненулевых строк равно числу неизвестных, которых тоже четыре).
Теперь выполним обратный ход метода Гаусса. Используя полученную трапециевидную матрицу, выразим последовательно все неизвестные, начиная с последней строки, то есть с 
.
Матрица 
соответствует системе
.
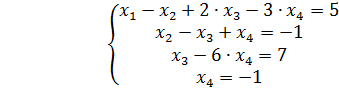В обратном порядке 
;
;
.
Решением системы является упорядоченный набор чисел 
.
Метод Гаусса является универсальным и может быть использован для решения любых совместных систем и для определения того, что система не имеет решений в случае ее несовместности.
2. Метод Крамера используется только для решения квадратных систем линейных алгебраических уравнений, которые имеют невырожденную основную матрицу.
Рассмотрим квадратную систему 
.
Если эта система невырожденная, то есть определитель ее основной матрицы не равен нулю, тогда систему можно решить, вычислив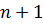 
определитель 
порядка. Неизвестные определяются по формулам Крамера 
. Один из этих определителей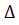 
- определитель основной матрицы, 
– определители, которые получают заменой 
столбца в определителе основной матрицы системы столбцом свободных членов:
;
;
;
.
Рассмотрим пример решения системы 
методом Крамера.
Найдем определители: 
;
; 
;
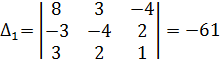Неизвестные найдем по формулам Крамера:
3. Матричный метод решения систем линейных алгебраических уравнений.
Матричный метод также как и метод Крамера может быть использован лишь для решения квадратных систем вида (2), имеющих невырожденную основную матрицу.
Для решения системы этим методом ее записывают в матричной форме: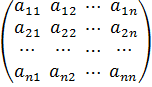 
. Другими словами, систему линейных алгебраических уравнений представляют как матричное уравнение вида 
и решают соответственно. Умножают обе части равенства слева на матрицу, обратную основной матрице 
. Таким образом, определяют матрицу-столбец неизвестных:
Рассмотрим пример решения системы 
матричным методом. Представим систему как матричное уравнение:
и найдем неизвестные .
Найдем матрицу 
, обратную основной матрице 
,
.
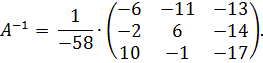
Решением системы являются числа 
Дата добавления: 2015-04-20; просмотров: 17 | Поможем написать вашу работу | Нарушение авторских прав |