Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА

Теорема 1. Если f (x) С[ a; b ], а F (x) – какая-либо ее первообразная на [ a; b ] (Fʹ (x)= f (x)), то справедливо выражение

. (1)

Док. _▼

Рассмотрим разбиение отрезка [ a; b ] на частичные отрезки.

Также рассмотрим равенство

F (b) – F (a) =(F (x_n) – F (x_{n –1})) +(F (x_{n –1}) – F (x_{n –2})) +… + (F (x ₂) – F (x ₁)) + (F (x ₁) – F (x ₀)).

Преобразуем каждую разность в соответствии с теоремой Лагранжа

(если F (x) С¹(a; b), то с (a; b):

F (b) – F (a) = Fʹ (с)(b – a)).

Получим

F (b) – F (a)= Fʹ (с_n)(x_n – x_{n –1})+ Fʹ (с_{n –1})(x_{n –1} – x_{n –2})+ …+ Fʹ (с ₂)(x ₂ – x ₁) + Fʹ (с ₁)(x ₁ – x ₀) =

= ,

т.е.

,

где с_i (x_{i –1}; x_i).

Переходя к пределу при , получаем

или

.

^▲

Выражение (1) называется формулой Ньютона-Лейбница.

Пример 1. Вычислить

Решение _▼

.

^▲

4. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Свойства определенного интеграла.

1. .

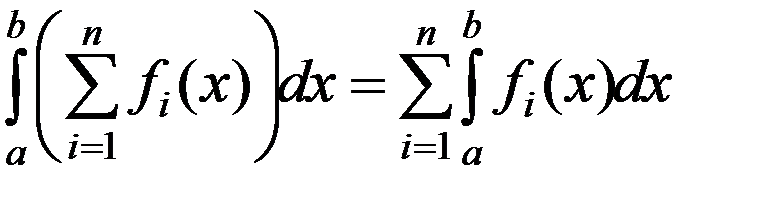2. , с = const.

3. .

Док. _▼

.

^▲

4. (Свойство аддитивности). Если функция f (x) интегрируема на [ a; b ] и a < с < b, то

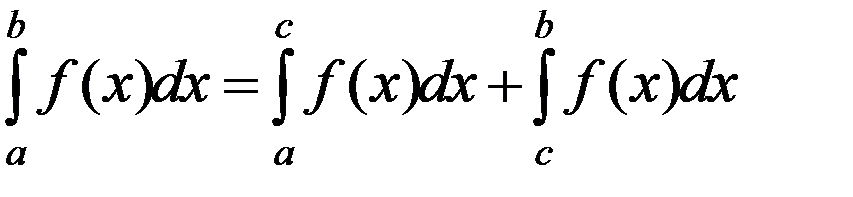. (1)

Док. _▼ Пусть точка с будет точкой деления при разбиении [ a; b ] на частичные отрезки (пусть с = x_m). Тогда интегральная сумма может быть представлена в виде двух сумм:

. (2)

Каждая из сумм в выражении (2) является интегральной для отрезков [ a; b ], [ a; с ], [ с; b ] соответственно.

Переходя к пределу в выражении (2) при 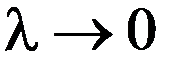, получаем (1).

^▲

Свойство аддитивности справедливо при любом расположении точек a, b, с. Например, если a < b < с, то

.

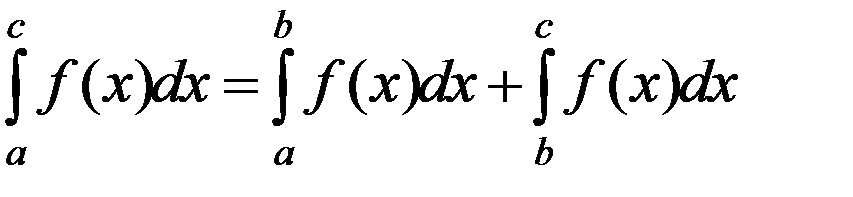Отсюда

.

(вытекает из свойств 4 и 3).

5. (Теорема о среднем). Если f (x) С[ a; b ], то [ a; b ]:

.

Док. _▼ По формуле Ньютона-Лейбница:

,

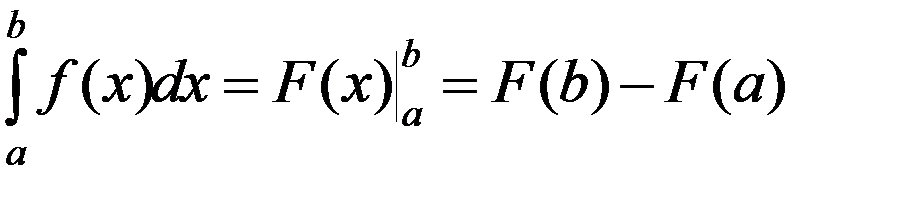где Fʹ (x) = f (x).

Применяем к разности F (b) – F (a) теорему Лагранжа:

.

^▲

Свойство 5 при f (x) ≥0 имеет простой геометрический смысл: значение определенного интеграла равно, при некотором с (a; b), площади прямоугольника с высотой f (с) и основанием b – a.

Число

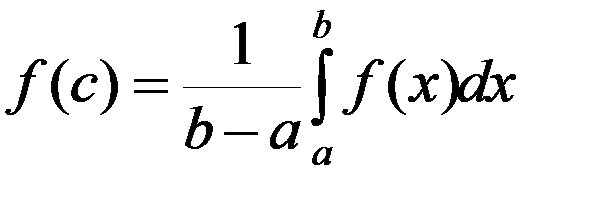
называется средним значением функции на [ a; b ].

6. Если f (x) сохраняет знак на [ a; b ], где a < b, то интеграл имеет тот же знак, что и функция.

Док. _▼ Пусть f (x) ≥0. По теореме о среднем

,

где с [ a; b ].

Так как f (x) ≥0 [ a; b ], то f (с) ≥0.

.

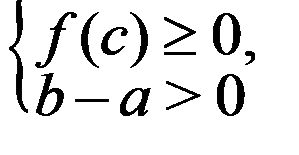
При f (x) ≤0 доказательство аналогично.

^▲

7. Неравенства между непрерывными функциями на [ a; b ] (a < b) можно интегрировать.

Если f ₁(x) ≤ f ₂(x), x [ a; b ], то

.

(Дифференцировать неравенства нельзя).

8. (Оценка интеграла). Если

, , то

. (3)

Док. _▼

m ≤ f (x) ≤ M [ a; b ]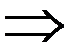

(свойство 7).

Учитывая, что

, ,

следует выражение (3).

^▲

9. Модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции:

.

Док. _▼ Применяем свойство 7 к известным неравенствам

получаем

.

В соответствии со свойствами модуля

.

^▲

10. Производная от определенного интеграла равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом:

.

Док. _▼ По формуле Ньютона-Лейбница:

.

Следовательно

.

^▲