Читайте также:
|
Теорема 8. Пусть C(m,n) обозначает число композиций числа n точно с m частями, тогда C(m,n)=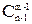 
.
Доказательство 1.
Рассуждение, используемое в доказательстве теоремы 4, можно легко применить для доказательства того, что
= (t1+ t2+ t3+ t4+…)m= 
=tm 
= 
= 
.
Приравнивая коэффициенты при tn в крайних членах этой цепочки равенств, получаем требуемое.
Доказательство 2.
Введем графическое представление для композиций числа n. C композицией (a1a2…am) числа n связываем m сегментов интервала [0, n]; первый сегмент имеет длину а1, второй – длину а2 и т. д. Например, композиция (3 2 3 1 2) числа 11 представим в виде
0←1─2→3←4→5←6─7→8↔9←10→11
Заметим теперь, что можно построить каждую из С(m,n) композиций числа n c m частями, выбирая m-1 чисел из n-1 первых целых как конечные точки для таких m сегментов, разделяющих интервал [0, n]. Поскольку таких выборов может быть 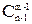, видим, что C(m,n)= .
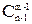Простота теоремы 6 позволяет получать чисто асимптотические выражения для некоторых функций разбиений, связывая их с функциями композиций. Например,
Теорема 9. (Эрдеш – Ленер). Пусть РM(n) обозначает число разбиений числа n ровно с М частями, тогда при n→∞
РM(n)≈ 
, если M=o(n1/3).
Задачи
1.Пусть Fn – n-е число Фибоначчи F0=0, F1=1, Fn=Fn-1+Fn-2, n>1. Показать, что число композиций n, в которых нет единиц, равно Fn-1.
2. В более общем виде – Пусть kFn – определяется по правилу;
kF0=…=kFk-2, kFk-1=1, kFn=kFn-1+kFn-k.
Показать, что число композиций n, в которых все части ≥ k, равно kFn-1.
3. Из задачи 2 следует, имеется 2n-1 композиций числа n.
4. пусть Сk(m,n) обозначает число композиций n точно с m частями, каждая из которых не меньше k. Тогда
Сk(m,n)=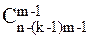 
5. Из задач 2 и 4 следует, что
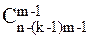= kFn-1
Дата добавления: 2015-09-11; просмотров: 56 | Поможем написать вашу работу | Нарушение авторских прав |