Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Упражнение. Выполните приведенный алгоритм для деревьв

а) b)

1 7 1 7

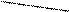
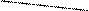
8 2 3 2 8 3

5 5

6 6

4 4

Заметим, что в приведенном алгоритме, построенный им код определен однозначно.

Рассмотрим алгоритм восстановления дерево по его коду Прюфера i₁,…,i_n-2. Для этого

1. Восстановим заключительное звено дерева. Как было отмечено, им является ребра либо (i_n-2,n), в случае i_n-2¹n, либо ребро – (n,n-1), в случае i_n-2=n.

2. Для восстановления других ребер дерева выполним следующее

2.1 Пусть j=n-2.

2.2 Повторим n-2 раза

Если вершина i_j-1 (исключая j=1) еще не включена в дерево, то строим в нем ребро (i_j,i_j-1); в противном случае строим ребро (i_j,m), где m наибольший номер вершины еще не включенной в дерево.

Упражнение. Восстановите деревья по кодам Прюфера, полученным в предыдущем упражнении.

Замечание. Пусть задана произвольная последовательность натуральных чисел i₁,…,i_n-2, каждое из которых из промежутка 1..n. Тогда, по приведенному алгоритму, для этой последовательности может быть построено помеченное дерево, при этом двум разным последовательностям соответствуют два разных дерева.

Таким образом, теорема Кэли следует из установленной биекции.

Третий подход (Пойа 1937). Экспоненциальная производящая функция для числа помеченных корневых деревьев может быть задана выражением

y = 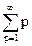t_p t ^p/p!. (19)

Пойа нашел функциональное уравнение для у, как функции от t, и затем для нахождения t_p применил формулу обращения Лагранжа.

Это функциональное уравнение для y будет сейчас выведено. Из леммы пересчета помеченных графов следует, что yⁿ/n! является экспоненциальной производящей функцией для n-множеств помеченных корневых деревьев. Эти n-множества соответствуют в точности тем корневым деревьям, в которых корень имеет степень n и не помечен. Более точно, это соответствие получается так: сначала добавляем к каждому n-множеству новую вершину, не помечая ее, а затем соединяем эту новую вершину с каждым из старых корней. Умножение выражения yⁿ/n! на t отвечает приписыванию пометки новому корню и включению его в число пересчитываемых вершин. Таким образом, t yⁿ/n! перечисляет корневые помеченные деревья, в которых корень имеет степень n. Суммируя по n, получаем

y = yⁿ/n!, (20)

и, следовательно, мы приходим к функциональному уравнению

y= te^y (21)

чтобы найти решение (20), выразив y как функцию от x, мы применим весьма полезный частный случай формулы Лагранжа.

Формула обращения Лагранжа (частный случай)[8]. Если функция j(y) аналитична в некоторой окрестности точки y=0 и j(0)¹0, то уравнение

t=y/j(y) (22)

имеет единственное решение, задаваемое производящей функцией

y = (23)

коэффициенты которой определяются по формуле

c_k = (1/k!){(d/dy)^k-1(j(y))^k}_y=0. (24)

Применяя эту формулу обращения к уравнению (21), где j(y)=e^y, находим

y = t^k/k!, (25

и, сравнивая это выражение с (19), снова получаем формулу для t_p.

Четвертый подход (Кирхгоф 1847) Более интересный и полезный результат, обычно называемый “Матричная теорема о деревьях” содержится в работе Кирхгофа 1847 года. Число помеченных деревьев может быть быстро получено как простое следствие этого результата.

Пусть А=(G)+ça_ij ç – матрица смежности графа G. обозначим М(G) матрицу, которая получается из –A с помощью подстановки на место i-го диагонального элемента в ней числа deg v_i, для каждого i.

Теорема. (Матричная теорема о деревьях для графов). Для всякого связного помеченного графа G все алгебраические дополнения матрицы М(G) равны друг другу и их общее значение представляет собой число остовных деревьев графа G.

Для иллюстрации этой сформулированного утверждения рассмотрим

М(G)= , M(G)= − = 3.

Теорема Кэли является следствием применения матричной теоремы о деревьях к полном графу K_p. В самом деле, алгебраическое дополнение M(K_p) равно

− = p^p-2

(Для вычисления определителя. Вычитаем первую строку из каждой другой и прибавляем последние р-2 столбцов к первому. Получается верхняя треугольная матрица, определитель которой равен p^p-2.)

Доказательство (Матричной теоремы о деревьях для графов[9])

Лемма 1. Пусть B – произвольная числовая n´n-матрица, в каждой строке которой и в каждом столбце сумма элементов равна нулю:

=0, i=1,…,n; =0, j=1,…,n.

Тогда алгебраические дополнения всех элементов матрицы B равны между собой. (В частности, этим свойством обладает матрица Кирхгофа произвольного графа.

Доказательство

Очевидно, что rank B<n. если rank< n-1, то алгебраические дополнения всех элементов матрицы равны 0. Пусть rank= n-1 и С – присоединенная матрица для матрицы B, т. е. элемент C_ij равен алгебраическому дополнению A_ij

элемента B_ij в матрице B, i=1,…,n; j=1,…,n. Известно, что BC=(det B)E, где E – единичная матрица. В наших условиях det B = 0, ВС = 0 – нулевая матрица. Следовательно, для столбца матрицы C с номером j, j=1,…,n, верны равенства

B_i1C_1j+ B_i2C_2j+…+ B_inC_nj=0, i=1,…,n,

т.е.

B_i1А_j1+ B_i2А_j2+…+ B_inА_jn=0, i=1,…,n,

Эти равенства можно рассматривать как систему линейных однородных уравнений с матрицей B относительно неизвестных А_j1, А_j2,…, А_jn. Так как rank B = n-1, то все решения системы пропорциональны. Но вектор (1,…,1) удовлетворяет системе, поэтому

А_j1= А_j2=…=А_jn j=1,…,n.

Учитывая, что CB = 0, аналогично получаем

А_1i= А_2i=…=А_ni i=1,…,n.

Следовательно,

А_ij= А_kl, i, j, k, l=1,…,n.

Определение. Пусть G – (n, m)-граф, n´ m-матрица I =I(G) называется матрицей инцидентности графа G, если I удовлетворяет условиям:

Для неориентированных графов

I_kl=

Для ориентированных графов

I_kl=

Пусть G – неориентированный граф. Превратим каждое его ребро в дугу, придав ему одну из двух возможных ориентаций. Полученный ориентированный граф называется ориентацией графа G. Непосредственно проверяется

Утверждение Если М(G) – матрица Кирхгофа графа G, а I – матрица инцидентности какой-либо его ориентации H (нумерация вершин в H та же, что и вG), то М(G)=I I^tr (здесь tr – операция транспонирования матрицы).

Лемма 2. Пусть H – (m+1, m)-граф, I – матрица инцидентности какой-либо его ориентации, M – произвольный минор порядка m матрицы I. Тогда

1) если H – дерево, то M = ±1;

2) если H не является деревом, то M =0.

Доказательство

Прежде всего заметим, что можно произвольно менять нумерации вершин и ребер графа Н, от этого рассматриваемый минор может лишь изменить знак.

Пусть а – вершина, соответствующая строке матрицы I, не вошедшей в минор M. Если граф H не является деревом, то он несвязен. Пусть K={1,2,…,k} – его область связности, не содержащая вершины a. С помощью подходящей перенумерации ребер графа H матрицу I приведем к клеточно-диагональному виду I=diag[ I₁,I₂], где I₁ – матрица инцидентности компоненты H(K). Минор M содержит все первые к строк матрицы I, сумма которых равна нулевой строке. Следовательно, M=0.

Пусть теперь H – дерево. Заново перенумеруем вершины и ребра графа Н следующим образом. Одной из концевых вершин v, отличных от вершины a, а также ребру инцидентному вершине v, присвоим номер 1. Далее рассмотрим дерево T₁= H-v. если его порядок больше 1, то одной из его концевых вершин u, отличных от a, а также инцидентному ей ребру присвоим номер 2. Рассмотрим дерево T₂= T₁ –u. Итерируя этот процесс, получим новые нумерации вершин и ребер дерева H, причем вершина a будет иметь номер m+1. Матрица I при этом помет вид

.

(Здесь символ * обозначает те элементы или блоки матрицы, значения которых не влияют на ход рассуждений.) Минор М, остающийся после удаления последней строки этой матрицы, равен ± 1.

Для доказательства теоремы Кирхгофа мы также воспользуемся формулой Бинэ – Коши, доказательство которой обычно приводится в любом достаточно полном курсе по теории матриц[10]. Пусть A и В – n´ m- и m ´ n- матрицы соответственно, С=АB и n≤m. Минор порядка n матрицы B назовем соответствующим минору порядка n матрицы A, если множество номеров строк первого из них и номеров столбцов второго совпадают.

Формула Бинэ – Коши. Определитель матрицы C равен сумме произведений каждого минора порядка n матрицы A на соответствующий минор матрицы B.

Доказательство теоремы Кирхгофа.

Пусть I – матрица инцидентности какой-либо его ориентации (n,m)-графа G. Имеем

М(G)=I∙I^tr. (*)

Поскольку G – связный граф, m≥n-1. Если B – подматрица, остающаяся после удаления из М(G) последних строки и столбца, С – подматрица, остающаяся после удаления из I последней строки, то в силу (*) B=C∙C^tr. Алгебраическое дополнение А_nn равно det B. Из формулы Бинэ – Коши теперь следует, что А_nn равно сумме квадратов всех миноров порядка n-1матрицы С. Согласно, леммы 1 каждый такой минор М равен ±1, если остовной подграф графа G, ребра которого соответствуют столбцам, вошедшим в M, является деревом, и нулю в противном случае. Следовательно, А_nn равно остовных деревьев в графе G. Поскольку алгебраические дополнения всех элементов матрицы М(G) равны (лемма 2), то теорема доказана.