Читайте также:
|
Пусть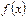 
и 
- функции, для которых существуют пределы при 
(
): 
, 
.
Сформулируем основные теоремы о пределах:
1) Функция не может иметь более одного предела.
Предположим противное, т.е. что функция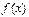 
имеет 2 предела А и D, 
. Тогда на основании теоремы о связи бесконечно малых величин с пределами функции: 
, 
, где 
и 
- бесконечно малые величины при (). Вычитая почленно эти равенства, получим: 
, откуда 
. Это равенство невозможно, т.к. на основании свойства 1 бесконечно малых 
это величина бесконечно малая. Следовательно, предположение о существовании второго предела неверно.
2) Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е.
.
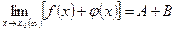3) Предел произведения конечного числа функций равен произведению пределов этих функций, т.е.
.
По условию и , следовательно, на основании теоремы о связи бесконечно малых величин с пределами функции: , 
, где и - бесконечно малые величины при (). Перемножая почленно оба равенства, получим:
.
На основании свойств бесконечно малых последние три слагаемые представляют величину, бесконечно малую 
при ().
Итак, функция 
представляет сумму постоянного числа 
и бесконечного малой . На основании обратной теоремы о связи бесконечно малых с пределами функции это означает, что 
.
В частности, постоянный множитель можно выносить за знак предела, т.е.
.
Дата добавления: 2015-09-11; просмотров: 30 | Поможем написать вашу работу | Нарушение авторских прав |