Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Задача о касательной

Пусть на плоскости дана непрерывная функция и необходимо найти уравнение касательной к этой кривой в точке .

Уравнение прямой по точке , принадлежащей этой прямой, и угловому коэффициенту имеет вид: , где , ( - угол наклона прямой). Из (рис.5.1) найдем тангенс угла наклона секущей : . Если точку приближать к точке , то угол будет стремиться к углу , т.е. при . Следовательно, .

Из задачи о касательной следует геометрический смысл производной: производная f′ (x ₀) есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой у=f′ (x) в точке х ₀, т.е. k= f′ (x ₀).

Следовательно, уравнение касательной к кривой y=f (x) в точке х ₀ примет вид

Пример. Найти производную функции f (x)= х ².

Решение. Придавая аргументу х приращение ∆ х, найдем соответствующее приращение функции:

Составим отношение:

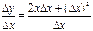
Найдем предел этого отношения при ∆ х → 0: