Читайте также:
|
Значение слова "Конечных приращений формула"
Конечных приращений формула, формула Лагранжа, одна из основных формул дифференциального исчисления, дающая связь между приращением функции f(x) и значениями её производной, эта формула имеет вид:
f(b)-f(a)=(b-a)f’(c), (1)
где с — некоторое число, удовлетворяющее неравенствам a<с<b. Формула (1) справедлива, если функция f(x) непрерывна на отрезке [ a, b ] и имеет производную в каждой точке интервала (а, b). Геометрически формула (1) выражает, что на кривой y = f(x) найдётся точка [ c, f(c) ], касательная в которой параллельна хорде, проходящей через точки [ a, f(a) ]и [ b, f(b) ]. К. п. ф. была открыта Ж. Лагранжем в 1797.
Среди различных обобщений К. п. ф. следует отметить формулу Бонне
,
её частный случай — формулу Коши
.
Рис. к ст. Конечных приращений формула.
Раскрытие неопределённостей вида 
, 
Определение (« на языке последовательностей », или по Гейне)
Число А называется пределом функции y=f (x) в точке х 0 (или при 
), если для любой последовательности допустимых значений аргумента xn, 
, сходящейся к х 0 (т.е. 
), последовательность соответствующих значений функции f (xn), сходится к числу А (т.е. 
).
Определение (на « языке ε-δ », или по Коши»)
Число А называется пределом функции y=f (x) в точке х 0 (или при , т.е. 
), если для любого положительно ε найдётся такое положительное число δ, что при всех 
, удовлетворяющих неравенству 
, выполняется неравенство 
.
Основные теоремы о пределах
Теорема 1.
Предел суммы (разности) двух функций равен сумме (разности) их пределов:
Следствие. Функция может иметь только один предел при .
Теорема 2. Предел произведения двух функций равен произведению их пределов:
Теоремы 1 и 2 справедливы для любого конечного числа функций.
Следствие. Постоянный множитель можно выносить за знак предела:
Следствие. Предел степени с натуральным показателем равен той же степени предела:
Следствие. 
Теорема. Предел дроби равен пределу числителя, делённому на предел знаменателя, если предел знаменателя не равен нулю:
, (
)
При нахождении пределов применяют соотношения:
, (k =const); 
;
; 
;
; 
; 
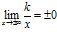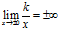(28).
Постановка задачи. Найти 
.
План решения. Для того чтобы найти вычисляем f (х 0), при этом:
§ если данное выражение имеет смысл, то предел равен этому выражению;
§ если в результате вычислений нет неопределённостей, воспользуемся одним из соотношений (28).
№9. Найти пределы: 1)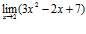 
; 2) 
;
3) 
.
► 1) Применяя теоремы о пределах, получаем:
= 
=
= 
;
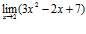2) Пределы числителя и знаменателя существуют и предел знаменателя не равен нулю. Пользуясь теоремой о пределе частного, находим: = 
;
3) Непосредственно применять теорему о пределе частного нельзя, так как предел знаменателя равен нулю (в знаменателе есть бесконечно малая величина при 
). В числителе имеем ограниченную величину, отличную от нуля. Таким образом, под знаком предела будет произведение ограниченной величины 
, отличной от нуля, на бесконечно большую величину 
при как величину, обратную бесконечно малой. Поэтому 
. ◄
Постановка задачи. Найти , где 
или 
.
План решения. Для того чтобы найти вычисляем f (х 0), если в результате вычислений получилась неопределённость 
или 
, следует применить соответствующие правила для раскрытия данных неопределённостей.
Неопределённость вида
§ Для того чтобы разрешить неопределённость вида , до вычисления предела средствами алгебры в числителе и знаменателе выделяем множитель 
и сокращаем на него, т.к. 
.
§ Чтобы раскрыть неопределённость , в которой числитель или знаменатель содержит иррациональность, следует соответствующим образом избавиться от иррациональности.
Неопределённость вида
§ Если числитель и знаменатель, сложные степенные функции: необходимо вынести за скобку в числителе и знаменателе дроби неизвестное с наибольшим показателем степени среди всех слагаемых дроби; после сокращения дроби неопределённость устраняется.
Частный случай: предел рационального выражения вида
при 
будем рассматривать как предел частного двух многочленов, который равен:
§ Если числитель и знаменатель, сложные показательные функции: за скобку вынести наиболее быстро возрастающее слагаемое среди всех слагаемых дроби; после сокращения дроби неопределённость устраняется.
№10. Найти пределы: 1) 
;2) 
; 3) 
.
► 1) = 
, для раскрытия данной неопределенности средствами алгебры разложим числитель и знаменатель на множители:
,
сократим множитель (х – 3) имеем:
= 
;
2) 
.
Данное предельное выражение содержит иррациональность в числителе, следовательно, домножим дробь на сопряженное выражение, т.е. на 
, тогда:
.
В числителе последнего выражения получилась формула — разность квадратов, таким образом:
;
3) 
,
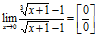для раскрытия данной неопределенности сделаем замену:
тогда исходное пределное выражение имеетвид:
,
которое раскрывается по известным правилам, т.е.:
= 
= 
. ◄
№11. Найти пределы: 1)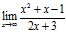 
; 2) 
;3) 
; 4) 
.
► 1) 
,
для раскрытия данной неопределенности разделим почленно числитель и знаменатель на х 2, тогда:
= 
;
2) 
,
для раскрытия данной неопределенности разделим почленно числитель и знаменатель на х 3, тогда:
;
3) 
,
для раскрытия данной неопределенности разделим почленно числитель и знаменатель на n 4, тогда:
= 
= 
;
4) 
= ,
для раскрытия данной неопределенности разделим почленно числитель и знаменатель на n, тогда:
= 
=0. ◄
№12. Найти пределы: 1) 
;
2) 
; 3) 
.
► Данные предельные соотношения можно рссмотреть, как частное двух многочленов, т.е:
1) 
= 
=2;
2) 
;
3) 
.◄
Постановка задачи. Найти .
План решения. Для того чтобы найти вычисляем f (х 0), если в результате вычислений получилась одна из неопределённостей 
, 
или др., то данные неопределённости раскрываются путём преобразования и сведения их к неопределённости или .
№13. Найти пределы: 1) 
; 2) 
.
► 1) 
,
данное предельное выражение преобразум таким образом:
= 
;
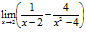2) Рассмотрим два случая:
а) 
. Перенеся иррациональность из числителя в знаменатель, получим:
= 
= 
=0;
б)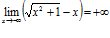 
.
Дата добавления: 2015-09-10; просмотров: 40 | Поможем написать вашу работу | Нарушение авторских прав |