
Читайте также:
|
| Определение Пр.1.4.1. |
Кривая, уравнение которой в некоторой ортонормированной системе координат имеет вид  , называется параболой. , называется параболой.
|
| Определение Пр.1.4.2. |
Точка  называется фокусом параболы.
Прямая называется фокусом параболы.
Прямая  называется директрисой параболы.
Число p называется фокальным параметром параболы. называется директрисой параболы.
Число p называется фокальным параметром параболы.
|
Свойства параболы иллюстрируются рис. Пр.1.4.1., на котором через 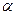 обозначим угол между касательной и фокальным радиусом, а через
обозначим угол между касательной и фокальным радиусом, а через 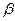 угол между касательной и положительным направлением оси абсцисс.
угол между касательной и положительным направлением оси абсцисс.
 y
y
B
D A

a
b O x
F


Рисунок Пр.1.4.1.
Свойства параболы:
1°. Парабола - неограниченная кривая, существующая для  ;
;
2°. Парабола L обладает осевой симметрией относительно оси Ox, что вытекает из отношения
 ,
,
очевидного для канонического уравнения параболы.
3°. Для параболы имеет место монотонное возрастание абсолютной величины ординаты при возрастании абсциссы, причем в нуле касательная к параболе вертикальна.
| Теорема Пр.1.4.1. | Пусть A = 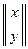 есть точка, принадлежащая параболе L, заданной каноническим уравнением, тогда имеют место следующие соотношения:
1°. есть точка, принадлежащая параболе L, заданной каноническим уравнением, тогда имеют место следующие соотношения:
1°.  ; 2°. ; 2°.  ;
3°. ;
3°.  ; 4°. ; 4°.  ;
5°. ;
5°.  . .
|
Доказательство:
1°. Имеем  , используя каноническое уравнение, получаем , используя каноническое уравнение, получаем  , но поскольку , но поскольку  , приходим сразу к справедливости утверждений 1° и 2°.
Справедливость 3° докажите самостоятельно.
4°. Наконец, , приходим сразу к справедливости утверждений 1° и 2°.
Справедливость 3° докажите самостоятельно.
4°. Наконец, 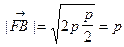 .
5°. Доказательство приводится после доказательства теоремы Пр.1.4.2.
Теорема доказана. .
5°. Доказательство приводится после доказательства теоремы Пр.1.4.2.
Теорема доказана.
|
Замечание о свойствах параболы
Каноническое уравнение, изучаемой в курсе элементарной математики параболы вида  , получается путем взаимного переименования координатных переменных.
, получается путем взаимного переименования координатных переменных.
Из теоремы Пр.1.4.1. следует возможность альтернативных формулировок свойств параболы.
Директориальное свойство параболы: парабола есть геометрическое место точек, отношение расстояния от которых до данной точки (фокуса) к расстоянию до данной прямой (директрисы) постоянно и равно единице.
Оптическое свойство параболы: касательная в любой точке гиперболы образует равные углы с фокальным радиусом точки касания и положительным направлением оси абсцисс. (Каждый луч света, выходящий из фокуса параболы, после отражения от параболы распространяется параллельно ее оси.)
Проведение касательных к параболе
| Теорема Пр.1.4.2. | Пусть A =  есть точка, принадлежащая параболе, заданной каноническим уравнением, тогда уравнение касательной к этой параболе, проходящей через точку А, имеет вид: есть точка, принадлежащая параболе, заданной каноническим уравнением, тогда уравнение касательной к этой параболе, проходящей через точку А, имеет вид:
 . .
|
Доказательство:
Уравнение касательной в точке A имеет вид 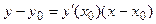 . Для параболы из канонического уравнения получаем . Для параболы из канонического уравнения получаем  , то есть , то есть  , ,  . Но тогда . Но тогда  , принимая во внимание, что , принимая во внимание, что  , окончательно получим , окончательно получим  .
Наконец, непосредственно проверяем утверждение теоремы для точки .
Наконец, непосредственно проверяем утверждение теоремы для точки  , где уравнение касательной , где уравнение касательной  .
Теорема доказана. .
Теорема доказана.
|
Доказательство свойства 5° теоремы Пр.1.4.1.:
Направляющий вектор касательной к параболе в точке A есть  , а вектор фокального радиуса - , а вектор фокального радиуса -  . Поэтому . Поэтому
 .
Но, с другой стороны, косинус угла .
Но, с другой стороны, косинус угла 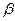 между векторами между векторами  и и  выражается той же формулой. Поскольку углы выражается той же формулой. Поскольку углы 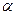 и и 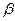 острые, то они равны.
Теорема доказана. острые, то они равны.
Теорема доказана.
|
Уравнение параболы в полярной системе координат
Поместим полюс полярной системы координат в фокус параболы, а полярную ось направим по линии, перпендикулярной директрисе и проходящей через ее фокус. (Рис. Пр.1.4.2.)
Для произвольной точки A, лежащей на параболе,
 .
Откуда .
Откуда 
|  y
A
r
O F j x
D
Рисунок Пр.1.4.2. y
A
r
O F j x
D
Рисунок Пр.1.4.2.
|
и окончательно  .
.
Дата добавления: 2015-09-10; просмотров: 31 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Пр.1.3. Гипербола и ее свойства | | | The role of Russia in overcoming of legal nihilism during armed conflicts |