
Читайте также:
|
Функция может терпеть разрыв на левом конце отрезка  , на правом конце или в некоторой внутренней точке с отрезка.
, на правом конце или в некоторой внутренней точке с отрезка.
Пусть функция 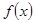 непрерывна на отрезке
непрерывна на отрезке  за исключением точки x= a, тогда несобственным интегралом второго рода от функции
за исключением точки x= a, тогда несобственным интегралом второго рода от функции 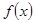 по отрезку
по отрезку 
 называется предел
называется предел  =
= 
.
Пусть функция 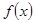 непрерывна на отрезке
непрерывна на отрезке  за исключением точки x= b, тогда несобственным интегралом второго рода от функции
за исключением точки x= b, тогда несобственным интегралом второго рода от функции 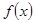 по отрезку
по отрезку 
 называется предел
называется предел  =
=  .
.
Пусть функция 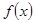 непрерывна на отрезке
непрерывна на отрезке  за исключением точки x=
за исключением точки x=  , тогда несобственным интегралом второго рода от функции
, тогда несобственным интегралом второго рода от функции 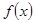 по отрезку
по отрезку  называется
называется  =
= 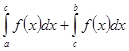 (интегралы в правой части определены выше).
(интегралы в правой части определены выше).
Если указанные пределы существуют и конечны, то интегралы называются сходящимися, если предел бесконечен или не существует вообще, то интеграл расходится.
Если сходятся интегралы от функций  , то сходятся интегралы от функций
, то сходятся интегралы от функций  . Это следует из теорем о пределах.
. Это следует из теорем о пределах.
Пример. 
 Интеграл расходится, так как пределы в правой части равенства бесконечны.
Интеграл расходится, так как пределы в правой части равенства бесконечны.
Заметим, если здесь формально применить формулу Ньютона-Лейбница (она неприменима, т.к. функция разрывна), получим ответ 2. Еще раз убеждаемся, что теоремы следует применять, внимательно проверяя условия их применимости.
Рассмотрим несобственный интеграл Дирихле второго рода  .
.
 .
.
При 
 , интеграл расходится.
, интеграл расходится.
Итак, несобственный интеграл Дирихле второго рода  сходится при
сходится при  расходится при
расходится при 
Замечание. Интегралы Дирихле первого и второго рода расходятся при n=1. При n>1 интеграл Дирихле первого рода сходится, а интеграл Дирихле второго рода расходится. При n<1 интеграл Дирихле первого рода расходится, а интеграл Дирихле второго рода сходится.
Признаки сравнения интегралов остаются верными и для интегралов второго рода. Эталонами сравнения служат обычно интегралы Дирихле и интегралы от показательной функции.
Примеры.  сходится сравнением с несобственным интегралом Дирихле
сходится сравнением с несобственным интегралом Дирихле  (n=
(n=  ) по второму признаку сравнения. Вспомните, что сумма бесконечно малых функций в знаменателе эквивалентна при
) по второму признаку сравнения. Вспомните, что сумма бесконечно малых функций в знаменателе эквивалентна при  бесконечно малой наинизшего порядка малости. Можно доказать эквивалентность непосредственным вычислением предела.
бесконечно малой наинизшего порядка малости. Можно доказать эквивалентность непосредственным вычислением предела.
 расходится сравнением с интегралом
расходится сравнением с интегралом  по второму признаку сравнения.
по второму признаку сравнения.
Дата добавления: 2015-09-10; просмотров: 36 | Поможем написать вашу работу | Нарушение авторских прав |