Читайте также:
|
Запишем уравнение автономной системы третьего порядка 
.
Все корни характеристического уравнения действительны и различны.
.
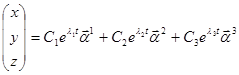Картину поведения фазовых траекторий довольно легко представить, рассматривая поведение фазовых траекторий в плоскостях, натянутых на пары собственных векторов. Этот случай уже изучен выше.
а) 
В плоскостях 
, 
, 
, имеем устойчивые узлы. Такая точка покоя так и называется – устойчивый узел.
б) 
В плоскостях , , , имеем неустойчивые узлы. Такая точка покоя называется – неустойчивый узел.
а) б)
в) один корень имеет знак, противоположный остальным двум корням. Точка покоя в этом случае называется седло – узел и является неустойчивой точкой покоя.
Пусть, например, 
. Тогда в плоскости имеем неустойчивый узел, а в плоскостях , - седла. Если 
, то в плоскости имеем устойчивый узел, а в плоскостях , - седла.
.
Заметим, что в ситуациях узлов и седла – узел траектория, начавшись в определенном октанте, не переходит в другой октант.
2) 
- действительный корень характеристического уравнения,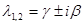 
- комплексно сопряженная пара корней.
Заметим, что при изменении номера корней ситуация будет аналогичной.
В плоскости имеем фокус, устойчивый при 
, неустойчивый при 
.
а) 
. Такая точка покоя называется устойчивый фокус.
б) 
. Такая точка покоя называется неустойчивый фокус.
в) или . Такая особая точка называется седло – фокус и является неустойчивой.
В первом случае по оси 
точка по траектории приближается к плоскости и уходит от начала координат, так как на самой плоскости имеем неустойчивый фокус.
Во втором случае на плоскости имеем устойчивый фокус, поэтому траектория стремится к оси , но удаляется от начала координат по этой оси, так как .
Дата добавления: 2015-09-10; просмотров: 22 | Поможем написать вашу работу | Нарушение авторских прав |