
Разделенные разности первого порядка 
Разделенные разности второго порядка  и т.д.
и т.д.
Разделенные разности 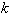 - го порядка:
- го порядка:
 (14)
(14)
Пусть  многочлен степени
многочлен степени 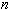 . Разность
. Разность  обращается в нуль при
обращается в нуль при 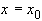 , следовательно, она делится на
, следовательно, она делится на  . Тогда разделенная разность первого порядка
. Тогда разделенная разность первого порядка  - многочлен степени
- многочлен степени  относительно
относительно 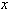 (и относительно
(и относительно 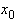 , так как выражение симметрично относительно
, так как выражение симметрично относительно 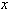 и
и 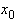 ).
).
Разность  обращается в нуль при
обращается в нуль при  , поэтому, разделенная разность второго порядка
, поэтому, разделенная разность второго порядка
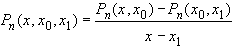 - многочлен степени
- многочлен степени  .
.
Аналогично,  - многочлен степени
- многочлен степени  и т.д.
и т.д.
Разделенная разность порядка n:  - многочлен нулевой степени.
- многочлен нулевой степени.
Разделенные разности более высокого порядка обращаются в нуль.
Значение  от
от 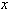 не зависит, тогда
не зависит, тогда 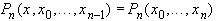
Из определения разделенных разностей следует:

и т.д.
Отсюда получаем формулу для  :
:
 (15)
(15)
Разделенные разности в соответствии с рекуррентной формулой (14) выражаются через значения многочлена в узлах  . Если
. Если  - узлы интерполяции,
- узлы интерполяции,  - значения интерполируемой функции в этих узлах, то они однозначно определяют интерполяционный многочлен степени
- значения интерполируемой функции в этих узлах, то они однозначно определяют интерполяционный многочлен степени 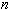 , значения которого в узлах совпадают с
, значения которого в узлах совпадают с  . Тогда разделенные разности многочлена
. Тогда разделенные разности многочлена  совпадают с разделенными разностями функции
совпадают с разделенными разностями функции  . Поэтому интерполяционный многочлен можно записать в форме:
. Поэтому интерполяционный многочлен можно записать в форме:
 (16)
(16)
Эта форма называется интерполяционным многочленом Ньютона с разделенными разностями.
Формула (17) более удобна для вычисления, чем запись интерполяционного многочлена в форме Лагранжа, т.к. добавление новых узлов интерполяции влечет вычисление только новых слагаемых, добавляемых к тому, что было вычислено с меньшим числом узлов. При использовании формы Лагранжа в этой ситуации требуется выполнять все вычисления заново.
[О комплексе|Теория|Практикум|Справочник по MathCAD'у|Об авторах]
[Home|Кафедра|ПетрГУ] 3.4. Численное дифференцирование.
Каждая из рассмотренных ранее интерполяционных формул может быть использована для приближенного нахождения значений производных функции 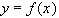 .
.
Дата добавления: 2015-09-12; просмотров: 18 | Поможем написать вашу работу | Нарушение авторских прав |