Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Властивості відношень

Відношення R називається рефлексивним, якщо для будь-якого а Î М має місце аRа. Головна діагональ його матриці містить тільки одиниці. Відношення R називається антирефлексивним, якщо ні для одного з аÎМ не виконується аRа. Головна діагональ його матриці містить тільки нулі.

Наприклад, відношення £ і “має спільний дільник” - рефлексивні, відношення < і “бути сином” - антирефлексивні.

Відношення R називається симетричним, якщо для пар (а, в)ÎМ² з аRв випливає вRа. Інакше кажучи, для довільної пари відношення R виконується або в обидві сторони або не виконується взагалі. Матриця симетричного відношення симетрична щодо головної діагоналі: a_ij = a_ji.

Приклад. Відношення "бути симетричним щодо осі Х".

Відношення R називається антисиметричним, якщо з a_i R a_j і a_j R a_i випливає, що a_i=a_j. Відношення ”бути симетричним": якщо перша точка симетрична другій, то і друга симетрична першій.

Приклад антисиметричного відношення: відношення £ дійсно, якщо а £ в і в£ а, то а=в. Неважко переконатися в тому, що відношення R симетрично тоді і тільки тоді, коли R=R^-1.

Відношення R називається транзитивним, якщо для будь-яких а, b і с із аRв і вRс випливає аRс. Відношення “рівність”, £, “жити в одному й тому ж місті” транзитивне; відношення “бути сином” не транзитивне.

Для будь-якого відношення R відношення 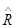, називане транзитивним замиканням R, визначається в такий спосіб: а 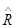в, якщо, у М існує ланцюжок із n елементів а = а₁, а₂, …, а_n-1, а_n = b, у якому між сусідніми елементами виконане R: а₁ R а₂, а₂ R а₃, ……, а_n-1 R в. Якщо R транзитивне, то 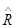= R. Дійсно, якщо а R в, то а 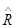в (ланцюжок складається з двох елементів а, в), тому RÍ 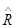. Якщо ж а 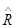в, то існує ланцюжок а₁ R а₂, а₂ R а₃,…, а_n-1 R в. Але оскільки R транзитивне, то а R в, тому 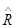Í R. З включення в обидві сторони випливає R= .

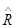Транзитивним замиканням відношення “бути сином” є відношення “бути прямим нащадком”, що є об'єднанням відношень “бути сином”, “бути онуком”, “бути правнуком” і т. д.

Відношення еквівалентності. Відношення називається відношенням еквівалентності, якщо воно рефлексивно, симетрично і транзитивне.

Приклад 1. Відношення рівності Е на будь-якій множині є відношенням еквівалентності. Рівність - це мінімальне відношення еквівалентності в тому сенсі, що при видаленні довільної пари з Е (тобто будь-якої одиниці на діагоналі матриці Е) воно перестає бути рефлексивним і, отже, уже не є еквівалентністю.

Приклад 2. Розглянемо множину трикутників на площині, рахуючи, що трикутник заданий, якщо задані координати його вершин. Два трикутники називаються рівними, якщо при накладенні вони збігаються, тобто можуть бути переведені одне в одне шляхом деякого переміщення. Відношення рівності (конгруентності) є відношенням еквівалентності на множині трикутників.

Приклад 3. Відношення “мати той самий залишок від ділення на 7” є еквівалентністю на множині цілих позитивних чисел N. Це відношення виконується, наприклад, для пар (11, 46), (14, 70) і не виконується для пар (12, 13), (14, 71).

Відношення називається відношенням нестрогого порядку, якщо воно рефлексивно, антисиметричне і транзитивне. Відношення суворого порядку - антирефлексивне, антисиметричне і транзитивне. Множина М, на якій задано відношення порядку, називається цілком упорядкованим, якщо будь-які два елементи М порівняні, і частково упорядкованим у противному випадку.

Приклад 4. Відношення £ і ³ для чисел є відношеннями нестрогого порядку, відношення < і > - відношеннями суворого порядку. Обидва типи відношень цілком упорядкують множину N.

Приклад 5. На системі підмножин множини М відношення включення Í задає нестрогий частковий порядок, а відношення суворого порядку включення Ì задає суворий порядок. Наприклад, {1, 2}Ì{1, 2, 3}, a {1, 2} і {1, 3, 4} не можуть порівнюватися.

Приклад 6. Відношення підпорядкованості на підприємстві задає суворий частковий порядок. У ньому непорівняними будуть співробітники різних відділів.

Приклад 7. Нехай у списку кінцевого алфавіту А порядок літер зафіксований, тобто завжди той самий. Тоді цей список визначає повне упорядкування літер, що назвемо відношенням передування й позначимо a_i 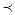a_j (якщо a_i передує a_j у списку літер). На відношенні передування літер будується відношення передування слів. Це відношення задає повне упорядкування множини усіх кінцевих слів в алфавіті А, що називається лексикографічним упорядкуванням слів. Прикладом такого упорядкування є словник.

Приклад 8. Якщо розглядати числа в позиційних системах числення (напр. десяткової) як слова в алфавіті цифр, то їх лексикографічне упорядкування збігається зі звичним, якщо всі числа, що порівнюються, мають однакове число розрядів. Наприклад:

20 < 1073;

20 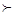1073;

0020 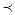1073.

Таким чином, відношення упорядкування для множин залежить від додаткових факторів, що пов'язані з характеристиками елементів цих множин.