Читайте также:
|
Рассмотрим множество расстояний между всеми парами кодовых слой в пространстве 
. Наименьший элемент этого множества называется минимальным расстоянием кода и обозначается 
. Как вы думаете, почему нас интересует именно минимальное расстояние, а не максимальное? Минимальное расстояние подобно наиболее слабому звену в цепи, оно дает нам меру минимальных возможностей кода и, следовательно, характеризует его мощность.
Как обсуждалось ранее, сумма двух произвольных кодовых слов дает другой элемент пространства кодовых слов. Это свойство линейных кодов формулируется просто: есл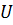и 
и 
— кодовые слова, то 
тоже должно быть кодовым словом. Следовательно, расстояние между двумя кодовыми словами равно весовому коэффициенту третьего кодового слова, т.е.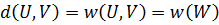 
. Таким образом, минимальное расстояние линейного кода можно определить, не прибегая к изучению расстояний между всеми комбинациями пар кодовых слов. Нам нужно лишь определить вес каждого кодового слова (за исключением нулевого вектора) в подпространстве; минимальный вес соответствует минимальному расстоянию . Иными словами, соответствует наименьшему из множества расстояний между нулевым кодовым словом и всеми остальными кодовыми словами.
Дата добавления: 2014-12-15; просмотров: 103 | Поможем написать вашу работу | Нарушение авторских прав |