Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Циклические коды. Важным подклассом линейных блочных кодов являются двоичные циклические коды

Важным подклассом линейных блочных кодов являются двоичные циклические коды. Код легко реализуется на регистре сдвига с обратной связью; на подобных регистрах сдвига с обратной связью вычисляется синдром; алгебраическая структура циклического кода естественным образом позволяет эффективно реализовать методы декодирования. Итак, линейный код (n, k) называется циклическим, если он обладает следующим свойством. Если n -кортеж является кодовым словом в подпространстве S, тогда , полученный из U с помощью циклического сдвига, также является кодовым словом в S. Или, вообще, , полученный i циклическими сдвигами, является кодовым словом в S.

Компоненты кодового слова можно рассматривать как коэффициенты полинома

Полиномиальную функцию можно рассматривать как "заполнитель" разрядов кодового слова 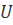, т.е. вектор n -кортежа описывается полиномом степени 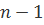или меньше. Наличие или отсутствие каких-либо членов в полиноме означает наличие 1 или 0 в соответствующем месте n -кортежа. Если 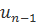-й компонент отличен от нуля, порядок полинома равен 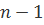. Удобство такого полиномиального представления кодового слова станет более понятным по мере дальнейшего обсуждения алгебраических свойств циклических кодов.