Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Элементарные отношения: тест Тарского, теорема Левенгейма

Среди проникающих ранений грудной клетки ранения сердца и перикарда встре­чаются в 10-15% случаев. Основным патофизиологическим моментом при ранениях серд­ца является поступление крови в полость перикарда, что затрудняет деятельность сердца (тампонада сердца). При этом вследствие одновременного сдавления коронарных сосудов резко нарушается питание сердечной мышцы. Кроме того, тампонада сердца может соче­таться со смещением средостения, перегибом сосудистого пучка и т.д.

Лечение. При ранениях сердца показана операция.

Техника операции. Под интубационным эндотрахеальным наркозом выполняется торакотомия, чаше всего переднебоковая в IV-V межреберьях, что обеспечивает необхо­димые условия для ревизии органов грудной клетки. Перикард вскрывают продольно кнутри от диафрагмального нерва. Рану сердца прикрывают пальцем для остановки кро­вотечения. Швы лучше всего накладывать атравматическими иглами. Можно использо­вать швы на тефлоновых прокладках. При расположении раны рядом с коронарной арте-

рией используются П-образные швы под венечной артерией. После ревизии полость пери­карда освобождают от крови и сгустков и ушивают редкими узловыми швами, оставляя небольшие окна в нижнем отделе. Плевральная полость дренируется, послойно ушивается наглухо, дренажи подключаются к аспирационной системе.

Трансплантация сердца

К настоящему времени выполнено более 10000 операций. Первая успешная орто-топическая трансплантация была произведена в декабре 1967 года Кристианом Барнардом (С. Barnard).

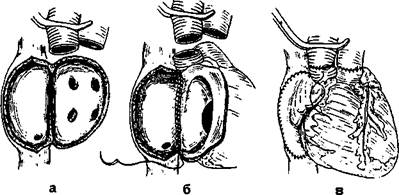
Рис. 12. Трансплантация сердца:

а) сердце реципиента удалено; б) начальный этап подшивания донорского сердца; в) заключительный этап трансплантации

Показания и противопоказания к операции. Заключение о том, нуждается ли больной в пересадке сердца, может быть сделано только в том случае, если имеются фак­торы, указывающие, что он (больной) по состоянию миокарда находится в терминальной стадии декомпенсации кровообращения. Абсолютными противопоказаниями к трансплан­тации сердца являются выраженная легочная гипертензия, инфекционные заболевания или другие заболевания, представляющие угрозу для жизни (опухоли и т.п.), повторные инфаркты легкого, инсулинзависимый диабет. Противопоказанием является также возраст больного (не должен превышать 60 лет).

Техника операции. Доступ к сердцу реципиента осуществляется из срединной стернотомии с использованием ИК. Иссекают пораженное сердце с пересечением обоих предсердий максимально близко к предсердие-желудочковой борозде с оставлением части межпредсердной перегородки; аорту и легочную артерию пересекают как можно ближе к полулунным клапанам. Обязательным условием операции является удаление ушек обоих предсердий (рис. 12а). Забор донорского сердца осуществляется второй бригадой хирур­гов в условиях холодовой кардиоплегии. Извлекают сердце после пересечения крупных магистральных стволов и немедленно помешают в изотонический раствор NaCl при тем­пературе +4° С. Операция по пришиванию донорского сердца выполняется в следующей последовательности: пришивают левое предсердие, межпредсердную перегородку, правое предсердие, легочную артерию и аорту (рис. 12б,в). После снятия зажима с аорты и согре­вания больного ритм сердца, как правило, восстанавливается спонтанно, однако в ряде случаев приходится прибегать к дефибрилляции. Операцию заканчивают по общеприня­той методике с дренированием полости перикарда и переднего средостения.

Литература:

1. Сердечно-сосудистая хирургия. Под редакцией В.И.Бураковского, Л.А.Бокерия. Москва, Медицина., 1989 г., 751 с.

2. Оперативная хирургия. Под редакцией И. Литтманна. Будапешт, Изд-во АН Венгрии., 1981 г., 1175с.

3. Harlan B.J., Starr A., Harwin P.M. Manual of Cardiac Surgeri. Springer-Verlag New York, Inc., 1995., 378 p.

Элементарные отношения: тест Тарского, теорема Левенгейма

Если отношение S является расширением отношения R,, то элементарность этого расширения R, означает, что любой кортеж элементов из носителя отно­шения R, ("меньшее" отношение) удовлетворяет одним и тем же формулам в R, и в S; это свойство выражается следующей очень полезной теоремой, где, заметим, выполнимость подразумевается относительно "большего" отношения

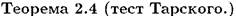Если S - расширение R. то это расширение элементарно тогда и только тогда, когда для любого а из носителя отноше­ния R и любой формулы 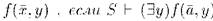, то существует b из носителя R, такой, что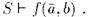

Необходимость очевидна. Достаточность докажем ин­дукцией по кванторному рангу р формулы : если из носителя R, тогда Это очевидно для р = 0, поскольку по определению самого понятия расширения удовлетворяет одним и тем же формулам в R и S. Предположим, что имеет вид 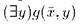, где кванторный ранг формулы g меньше р. Если , то по предположению существует b из носителя R, такой, что и по индукционному предположению 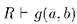, следовательно, 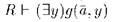. Если , то для всех b из носителя S и, в частности, для всех b из носителя R, имеем . По предположению индукции 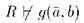, значит, Это завершает доказательство, поскольку формула кванторного ранга р является булевой комбинацией формул рассмотренного вида

□

Теорема 2.5 (теорема Левенгейма.) Каждое отношение R, имеет конеч­ное или счетное элементарное ограничение; более точно, если А - бесконечное подмножество носителя R,. то существует элементарное ограничение R,. носитель которого содержит А и равномощен А.

Доказательство. Пересчитаем все формулы с параметрами в А: существует счётное множество формул 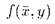; в каждой нужно заменить n -кой из А, и так как А бесконечно, то существует card(A) таких п-ок (по­скольку, если А бесконечно, то множество конечных подмножеств А имеет ту же мощность, что и А); значит, существует формул с параметрами из А (позднее мы уточним эту арифметику кардиналов). Для каждой формулы такой, что 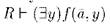, добавляем к А элемент b из носителя R, такой, что ; Так как нужно самое большее добавить card(A) элементов, то получим в итоге множество A₁, содержащее А и имеющее ту же мощность, что и А. Повторим эту операцию, заменив А на , получим множество и т.д. Пусть В - объединение множеств это - множество мощности , и ограничение R на В удовлетворяет условиям теста Тарского.

□

Мы видим, в частности, что каждая совместная теория языка m -арного от­ношения имеет конечную или счетную модель. Пусть I - носитель линейного порядка <; цепью расширений, индексированной множеством I, называется семейство отношений R_i с базой такое что расширение R_i для любых i < j. 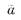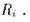Пределом (индуктивным!) цепи расширений называется един­ственное отношение R с базой являющееся расширением всех Ri: удовлетворяет R, если для достаточно большого i (на самом деле, как только попадает в ) удовлетворяет Очень часто на практике < полный порядок (например, порядок нату­ральных чисел , как в доказательстве теоремы 2.5), так как расширение строятся одно за другим; но это предположение не нужно для доказательства следующей теоремы.

Теорема 2.6 Если - це,пь элементарных расширений (т.е.

для i < j), то её предел R будет элементарным расширением каждого

Доказательство. Покажем индукцией по кванторному рангу р формулы 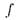, что если Это очевидно для р = 0. Пусть и g имеет кванторный ранг р. Если то существует b из E, такой, что 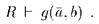Этот b принадлежит Ej для некоторого , и по гипотезе индукции . Значит, и, поскольку есть элементарное расширение 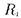, имеем Если , то для любого b из E и, в частности, для любого b из 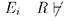, следовательно, по предположению индукции 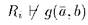, что влечёт