
Читайте также:
|
Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А. Очевидно, что угол j = w t + j0 где j0 - начальный угол.

Проекции вектора А на оси координат запишутся:


Видно, что проекции вращающегося вектора на оси координат по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу - начальную фазу.
Проводя аналогию дальше, можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:

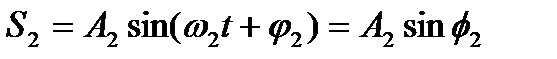
Сопоставим этим колебаниям два вектора А1 и А2, вращающихся с соответствующими угловыми скоростями.
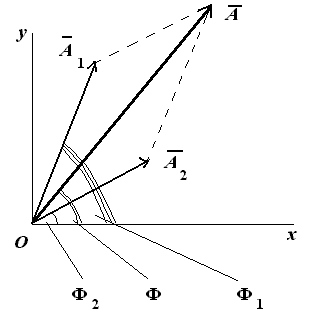
Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора А на ось y (амплитуда результирующего колебания) и угла f (фаза результирующего колебания).
Из очевидных геометрических соображений находим:

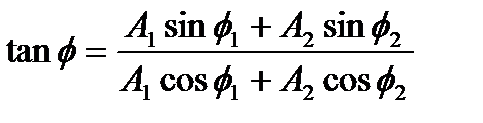
Отметим, что в общем случае сложения колебаний с разными частотами амплитуда результирующего колебания будет зависеть от времени. Если же частоты одинаковы, то 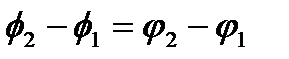 , то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:
, то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:

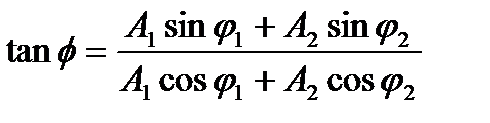
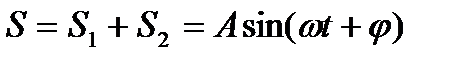
Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть  , и пусть для определенности
, и пусть для определенности 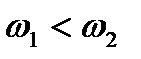 . Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний
. Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний
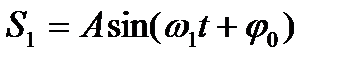
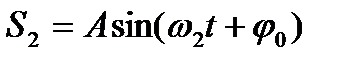
получим уравнение суммарного колебания:

Полученное результирующее колебание не является гармоническим (сравни с уравнением (1)); такого вида колебания носят название биений, название понятно, если посмотреть на график колебаний.
посмотреть на осциллографе
Величина, стоящая перед синусом, меняется со временем относительно медленно, так как разность частот мала. Эту величину условно называют амплитудой биений, а разность складываемых частот  - частотой биений (циклической).
- частотой биений (циклической).
При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x).
например, сложим два колебания с одинаковыми частотами:

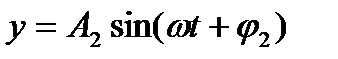
исключив время, получим:
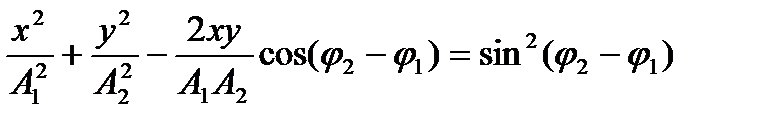
В общем случае это - уравнение эллипса. При A1=A2 - окружность, при 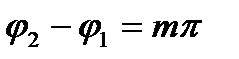 (m - целое) - отрезок прямой.
(m - целое) - отрезок прямой.
Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу
46.
Френель предложил оригинальный метод разбиения волновой поверхности S на зоны, позволивший сильно упростить решение задач (метод зон Френеля).
Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии от точки M (рис. 9.2). Точки сферы S, находящиеся на расстояниях,, и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля.
Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M.
Рис. 9.2
Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга:
| , | (9.2.2) |
где A – амплитуда результирующего колебания, – амплитуда колебаний, возбуждаемая i -й зоной Френеля.
Величина зависит от площади зоны и угла между нормалью к поверхности и прямой, направленной в точку M.
Площадь одной зоны
.
Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.
В то же время с увеличением номера зоны возрастает угол и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда. Она уменьшается также из-за увеличения расстояния до точки M:
.
Общее число зон Френеля, умещающихся на части сферы, обращенной в сторону точки M, очень велико: при,, число зон, а радиус первой зоны.
Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.
Световая волна распространяется прямолинейно. Фазы колебаний, возбуждаемые соседними зонами, отличаются на π. Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания от некоторой m -й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.
.
Тогда выражение (9.2.1) можно записать в виде
| . | (9.2.2) |
Так как площади соседних зон одинаковы, то выражения в скобках равны нулю, значит результирующая амплитуда.
Интенсивность излучения.
Таким образом, результирующая амплитуда, создаваемая в некоторой точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной, а интенсивность.
Так как радиус центральной зоны мал (), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно.
Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке M будет равна. Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к.). Интенсивность света увеличивается, если закрыть все четные зоны.
Таким образом, принцип Гюйгенса–Френеля позволяет объяснить прямолинейное распространение света в однородной среде.
Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонные пластинки – система чередующихся прозрачных и непрозрачных колец.
Опыт подтверждает, что с помощью зонных пластинок можно увеличить освещенность в точке М, подобно собирающей линзе.
47.
. Первое уравнение Максвелла представляет собой закон Гаусса (да, того самого Карла Гаусса, чьё имя носит колоколообразное распределение случайных величин; в те времена можно было быть и выдающимся математиком и выдающимся физиком одновременно) для электрических полей. Максвелл записал его в дифференциальной форме. В современной записи оно выглядит так (не пугайтесь математики, и не бросайте чтение хотя бы еще несколько абзацев):
∇· E = ρ/εo
где:
E – векторное электрическое поле (здесь и далее жирным шрифтом выделены векторные величины, а курсивом - скалярные);
∇· – значок оператора дивергенции (потока);
ρ – суммарный заряд;
ε o – диэлектрическая постоянная вакуума.
Первое уравнение говорит об очевидной вещи…
Но перед тем как ее озвучить, давайте разберемся, что такое дивергенция векторной величины. Вы видели водопроводный кран? Ну, тогда вы хорошо знаете, что такое дивергенция. В переводе с латинского это извержение наружу. Иначе говоря, поток. Для водопроводного крана это поток вытекающей воды, который тем больше, чем больше диаметр трубы и напор воды в ней. Если дивергенция больше нуля, то точка является источником, если меньше – стоком. Теперь вы знаете половину нужной векторной математики.
…Но вернемся к первому уравнению Максвелла (оно же – закон Гаусса). Оно говорит том, что поток электрического поля Е через любую замкнутую поверхность зависит от суммарного электрического заряда внутри этой поверхности. Иначе говоря, если из замкнутого бассейна вытекает воды больше, чем в него втекает (то есть суммарный поток из бассейна получается больше нуля), то ясно, что внутри бассейна прячется труба – источник этой самой воды (иначе бы она быстро кончилась).
С электрическим полем то же самое: если есть электрический заряд (труба-источник воды в бассейне), то поле от него будет вытекать наружу во все стороны (вода будет выливаться через края).
48.
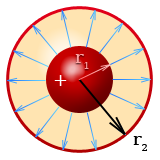
Сферический конденсатор состоит из двух концентрических полых сфер. Если расстояние между сферами ∆r очень мало, так что площадь обеих сферических поверхностей практически одинакова, то можно пользоваться выражением для емкости плоского конденсатора. Полагая S = 4πr2 см. площадь сферы, получаем:
| 1. | C =4 ·π·ε 0 ·ε
|
При большем расстоянии между поверхностями нужно учитывать различие площадей сфер.
Если
| C | емкость сферического конденсатора, | фарад |
| r1 | радиус внутренней сферы, | метр |
| r2 | радиус внешней сферы, | метр |
| εa | εa=ε0ε абсолютная диэлектрическая проницаемость, | Фарад/метр |
| ε0 | ε0=8.85·10-12электрическая постоянная, | Фарад/метр |
| ε | относительная диэлектрическая проницаемость, |
то
| 2. | C =4 πε 0 ε
|
49.
Геометри́ческая о́птика — раздел оптики, изучающий законы распространения света в прозрачных средах и принципы построения изображений при прохождении света в оптических системах без учёта его волновых свойств.
Краеугольным приближением геометрической оптики является понятие светового луча. В этом определении подразумевается, что направление потока лучистой энергии (ход светового луча) не зависит от поперечных размеров пучка света.
В силу того, что свет представляет собой волновое явление, имеет место интерференция, в результате которой ограниченный пучок света распространяется не в каком-то одном направлении, а имеет конечное угловое распределение т.е имеет место дифракция. Однако в тех случаях, когда характерные поперечные размеры пучков света достаточно велики по сравнению с длиной волны, можно пренебречь расходимостью пучка света и считать, что он распространяется в одном единственном направлении: вдоль светового луча.
В основе геометрической оптики лежат несколько простых эмпирических законов:
Поскольку геометрическая оптика не учитывает волновой природы света, в ней действует постулат, согласно которому если в какой-то точке сходятся две (или большее количество) систем лучей, то освещённости, создаваемые ими, складываются.
Однако наиболее последовательным является вывод законов геометрической оптики из волновой оптики в эйкональном приближении. В этом случае, основным уравнением геометрической оптики становится уравнение эйконала, которое допускает также словесную интерпретацию в виде принципа Ферма, из которого и выводятся перечисленные выше законы.
Частным видом геометрической оптики является матричная оптика.
50.
Звуковые колебания частиц упругой среды имеют сложный характер и могут быть представлены в виде функции времени a = a(t) (рис 3.1, а).

Рис.3.1. Колебания частиц воздуха.
Простейший процесс описывается синусоидой (рис. 3.1, б)
 ,
,
где amax - амплитуда колебаний; w = 2p f - угловая частота; f - частота колебаний.
Гармонические колебания с амплитудой amax и частотой f называются тоном.
Сложные колебания характеризуются эффективным значением на временном периоде Т
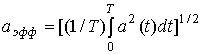 .
.
Для синусоидального процесса справедливо соотношение
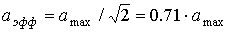 .
.
Для кривых другой формы отношение эффективного значения к максимальному составляет от 0 до 1.
В зависимости от способа возбуждения колебаний различают:
· плоскую звуковую волну, создаваемую плоской колеблющейся поверхностью;
· цилиндрическую звуковую волну, создаваемую радиально колеблющейся боковой поверхностью цилиндра;
· сферическую звуковую волну, создаваемую точечным источником колебаний типа пульсирующий шар.
Основными параметрами, характеризующими звуковую волну, являются:
· звуковое давление p зв, Па;
· интенсивность звука I, Вт/м2.
· длина звуковой волны l, м;
· скорость распространения волны с, м/с;
· частота колебаний f, Гц.
Если в сплошной среде возбудить колебания, то они расходятся во все стороны. Наглядным примером являются колебания волн на воде. При этом следует различать скорость распространения механических колебаний u (в нашем случае видимые поперечные колебания воды) и скорость распространения возмущающего действия с (продольные акустические колебания).
С физической точки зрения распространение колебаний состоит в передаче импульса движения от одной молекулы к другой. Благодаря упругим межмолекулярным связям движение каждой из них повторяет движение предыдущей. Передача импульса требует определенной затраты времени, в результате чего движение молекул в точках наблюдения происходит с запаздыванием по отношению к движению молекул в зоне возбуждения колебаний. Таким образом, колебания распространяются с определенной скоростью. Скорость распространения звуковой волны с - это физическое свойство среды.
Длина волны l равна длине пути, проходимого звуковой волной за один период Т:

где с - скорость звука, Т = 1 /f.
Звуковые колебания в воздухе приводят к его сжатию и разрежению. В областях сжатия давление воздуха возрастает, а в областях разрежения понижается. Разность между давлением, существующем в возмущенной среде p ср в данный момент, и атмосферным давлением p атм, называется звуковым давлением (рис.3.3). В акустике этот параметр является основным, через который определяются все остальные.
p зв = p ср - p атм. (3.1)

Рис.3.3. Звуковое давление
Среда, в которой распространяется звук, обладает удельным акустическим сопротивлением zA, которое измеряется в Па*с/м (или в кг/(м2*с) и представляет собой отношение звукового давления p зв к колебательной скорости частиц среды u
zA = p зв /u = r*с, (3.2)
где с - скорость звука, м; r - плотность среды, кг/м3.
Для различных сред значения zA различны.
Звуковая волна является носителем энергии в направлении своего движения. Количество энергии, переносимой звуковой волной за одну секунду через сечение площадью 1 м2, перпендикулярное направлению движения, называется интенсивностью звука. Интенсивность звука определяется отношением звукового давления к акустическому сопротивлению среды Вт/м2:
 (3.3)
(3.3)
Для сферической волны от источника звука с мощностью W, Вт интенсивность звука на поверхности сферы радиуса r равна
I = W / (4 p r 2),
то есть интенсивность сферической волны убывает с увеличением расстояния от источника звука. В случае плоской волны интенсивность звука не зависит от расстояния.
51.
Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида  в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний
в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний 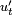 или её квадрата.
или её квадрата.
В акустике: затухание — уменьшение уровня сигнала до полной неслышимости.
Затухающие колебания пружинного маятника[править | править исходный текст]


Модель пружинного маятника. B — демпфер. F — внешняя сила (в примере не присутствует).
Пусть имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).
Тогда второй закон Ньютона для рассматриваемой системы запишется так:

где  — сила сопротивления,
— сила сопротивления,  — сила упругости
— сила упругости
 ,
,  , то есть
, то есть

или в дифференциальной форме
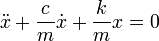
где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.
Для упрощения вводятся следующие обозначения: 
Величину 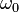 называют собственной частотой системы,
называют собственной частотой системы, 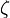 — коэффициентом затухания.
— коэффициентом затухания.
Тогда дифференциальное уравнение принимает вид
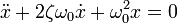
Сделав замену 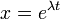 , получают характеристическое уравнение
, получают характеристическое уравнение
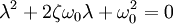
Корни которого вычисляются по следующей формуле

Решения[править | править исходный текст]


Зависимость графиков колебаний от значения 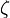 .
.
В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.
Если 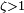 , то имеется два действительных корня, и решение дифференциального уравнения принимает вид:
, то имеется два действительных корня, и решение дифференциального уравнения принимает вид:

В этом случае колебания с самого начала экспоненциально затухают.
Если 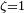 , два действительных корня совпадают
, два действительных корня совпадают  , и решением уравнения является:
, и решением уравнения является:
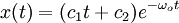
В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.
Если  , то решением характеристического уравнения являются два комплексно сопряжённых корня
, то решением характеристического уравнения являются два комплексно сопряжённых корня

Тогда решением исходного дифференциального уравнения является
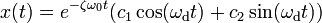
Где 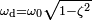 — собственная частота затухающих колебаний.
— собственная частота затухающих колебаний.
Константы  и
и  в каждом из случаев определяются из начальных условий:
в каждом из случаев определяются из начальных условий: 
52.
Дата добавления: 2015-01-30; просмотров: 60 | Поможем написать вашу работу | Нарушение авторских прав |