
Читайте также:
|
6.1 История задачи. В работах Д.К.Максвелла и И.А.Вышнеградского речь шла о САР, характеристические полиномы (многочлены) которых имели третью степень  . Условия устойчивости (отсутствие корней в правой полуплоскости комплексной плоскости корней) могли быть получены из формулы Кардано (Girolamo Cardano, 1501 - 1576). В наиболее завершенной форме условия устойчивости (
. Условия устойчивости (отсутствие корней в правой полуплоскости комплексной плоскости корней) могли быть получены из формулы Кардано (Girolamo Cardano, 1501 - 1576). В наиболее завершенной форме условия устойчивости (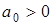 ,
, 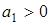 ,
,  ,
,  ,
,  ) были сформулированы Вышнеградским, и поэтому стали называться условиями (критерием) Вышнеградского.
) были сформулированы Вышнеградским, и поэтому стали называться условиями (критерием) Вышнеградского.
На заседании Лондонского математического общества в 1868 году Максвелл поставил задачу о разыскании условий для многочленов любой степени. Между тем эта задача фактически была решена еще в 1851 году французским математиком Ш.Эрмитом (Charles Hermite, 1822 - 1901). Однако результаты Эрмита не были доведены до практически удобных алгоритмов вычисления или формул и остались не известными специалистам, работающим в прикладных областях.
Задачу Максвелла решил в 1875 году английский математик и механик Э.Раус. Он указал удобный алгоритм, позволяющий для любого многочлена конечным числом простых арифметических действий определить условия устойчивости.
В конце 19 века А.Стодола, не зная работ Рауса, доказал необходимое условие устойчивости (положительность всех коэффициентов характеристического полинома) и поставил задачу об отыскании необходимых и достаточных условий перед выдающимся немецким (швейцарским) математиком А.Гурвицем (Adolf Hurwitz, 1859 - 1919). В 1895 году Гурвиц, опираясь на работы Эрмита, дал (независимое от Рауса) решение задачи в виде определенных условий (неравенств), накладываемых на коэффициенты полинома.
Это решение получило всеобщую известность и условия, найденные Гурвицем, стали называться критерием Рауса-Гурвица. В память о А.Гурвице многочлены, имеющие корни только в левой полуплоскости, стали называться гурвициевыми многочленами.
В настоящее время известны также и другие алгебраические критерии (критерий Соколова, критерий Льенара-Шипара), которые имеют меньшее число неравенств и более удобны при практических применениях.
Алгебраические критерии устойчивости применяются обычно для полиномов до 5 степени включительно, для полиномов более высоких степеней применяются частотные критерии, наиболее известными из которых являются критерий А.В.Михайлова и критерий Г.Найквиста.
Дата добавления: 2015-02-16; просмотров: 31 | Поможем написать вашу работу | Нарушение авторских прав |