
Читайте также:
|
-----------------------------------------------------------------------
1. Физический смысл уравнения Максвелла  заключается в следующем …
заключается в следующем …

| изменяющееся со временем магнитное поле порождает вихревое электрическое поле |
| источником вихревого магнитного поля помимо токов проводимости является изменяющееся со временем электрическое поле | |
| «магнитных зарядов» не существует: силовые линии магнитного поля замкнуты | |
| источником электрического поля являются свободные электрические заряды |
-----------------------------------------------------------------------
Решение:
Уравнение Максвелла  означает, что с переменным магнитным полем неразрывно связано вихревое электрическое поле.
означает, что с переменным магнитным полем неразрывно связано вихревое электрическое поле.
-----------------------------------------------------------------------
2. Физический смысл уравнения Максвелла 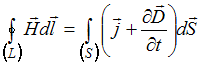 заключается в следующем …
заключается в следующем …

| источником вихревого магнитного поля помимо токов проводимости является изменяющееся со временем электрическое поле |
| изменяющееся со временем магнитное поле порождает вихревое электрическое поле | |
| «магнитных зарядов» не существует: силовые линии магнитного поля замкнуты | |
| источником электрического поля являются свободные электрические заряды |
-----------------------------------------------------------------------
Решение:
Из уравнения Максвелла 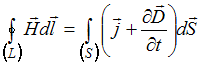 следует, что переменное электрическое поле, наряду с токами проводимости, является источником вихревого магнитного поля.
следует, что переменное электрическое поле, наряду с токами проводимости, является источником вихревого магнитного поля.
-----------------------------------------------------------------------
3. Физический смысл уравнения Максвелла 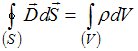 заключается в следующем …
заключается в следующем …

| источником электрического поля являются свободные электрические заряды |
| изменяющееся со временем магнитное поле порождает вихревое электрическое поле | |
| «магнитных зарядов» не существует: силовые линии магнитного поля замкнуты | |
| источником вихревого магнитного поля, помимо токов проводимости, является изменяющееся со временем электрическое поле |
-----------------------------------------------------------------------
Решение:
Данное уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде – источником электрического поля являются свободные электрические заряды. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.
-----------------------------------------------------------------------
4. Физический смысл уравнения Максвелла  заключается в следующем …
заключается в следующем …

| «магнитных зарядов» не существует: силовые линии магнитного поля замкнуты |
| изменяющееся со временем магнитное поле порождает вихревое электрическое поле | |
| источником электрического поля являются свободные электрические заряды | |
| источником вихревого магнитного поля помимо токов проводимости является изменяющееся со временем электрическое поле |
-----------------------------------------------------------------------
Решение:
Уравнение Максвелла  означает, что в природе нет магнитных зарядов, на которых начинались бы или заканчивались линии магнитной индукции.
означает, что в природе нет магнитных зарядов, на которых начинались бы или заканчивались линии магнитной индукции.
-----------------------------------------------------------------------
5. Уравнения Максвелла являются основными законами классической макроскопической электродинамики, сформулированными на основе обобщения важнейших законов электростатики и электромагнетизма. Эти уравнения в интегральной форме имеют вид:
1).  ;
;
2). 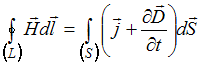 ;
;
3). 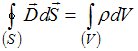 ;
;
4). 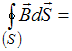 0.
0.
Третье уравнение Максвелла является обобщением …

| теоремы Остроградского – Гаусса для электростатического поля в среде |
| закона электромагнитной индукции | |
| закона полного тока в среде | |
| теоремы Остроградского – Гаусса для магнитного поля |
-----------------------------------------------------------------------
Решение:
Третье уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.
-----------------------------------------------------------------------
6. Уравнения Максвелла являются основными законами классической макроскопической электродинамики, сформулированными на основе обобщения важнейших законов электростатики и электромагнетизма. Эти уравнения в интегральной форме имеют вид:
1).  ;
;
2). 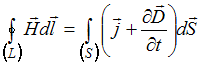 ;
;
3). 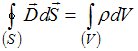 ;
;
4). 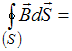 0.
0.
Четвертое уравнение Максвелла является обобщением …

| теоремы Остроградского – Гаусса для магнитного поля |
| закона электромагнитной индукции | |
| закона полного тока в среде | |
| теоремы Остроградского – Гаусса для электростатического поля в среде |
-----------------------------------------------------------------------
Решение:
Четвертое уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для магнитного поля. Максвелл предположил, что она справедлива для любого магнитного поля (в вакууме или в среде, стационарного и переменного).
-----------------------------------------------------------------------
7. Полная система уравнений Максвелла для электромагнитного поля в интегральной форме имеет вид:
 ,
,
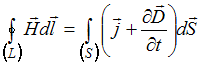 ,
,
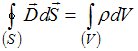 ,
,
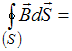 0.
0.
Следующая система уравнений:
 ,
,
 ,
,
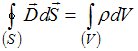 ,
,
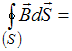 0 –
0 –
справедлива для …

| электромагнитного поля при наличии заряженных тел и в отсутствие токов проводимости |
| электромагнитного поля в отсутствие заряженных тел и токов проводимости | |
| стационарных электрических и магнитных полей | |
| электромагнитного поля при наличии заряженных тел и токов проводимости |
-----------------------------------------------------------------------
Решение:
Вторая система уравнений отличается от первой системы своими первым и вторым уравнениями. В первом уравнении иначе записана правая часть, но 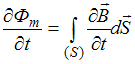 , а во втором уравнении отсутствует в подынтегральном выражении плотность тока проводимости
, а во втором уравнении отсутствует в подынтегральном выражении плотность тока проводимости 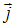 и не конкретизирована плотность тока смещения (
и не конкретизирована плотность тока смещения ( ). Отсутствие токов проводимости означает, что источником вихревого магнитного поля является только переменное электрическое поле. Таким образом, рассматриваемая система справедлива для переменного электромагнитного поля при наличии заряженных тел и в отсутствие токов проводимости.
). Отсутствие токов проводимости означает, что источником вихревого магнитного поля является только переменное электрическое поле. Таким образом, рассматриваемая система справедлива для переменного электромагнитного поля при наличии заряженных тел и в отсутствие токов проводимости.
-----------------------------------------------------------------------
8. Полная система уравнений Максвелла для электромагнитного поля в интегральной форме имеет вид:
 ,
,
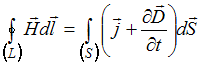 ,
,
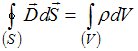 ,
,
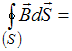 0.
0.
Следующая система уравнений:
 ,
,
 ,
,
 ,
,
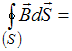 0 –
0 –
справедлива для …

| электромагнитного поля в отсутствие свободных зарядов |
| электромагнитного поля в отсутствие свободных зарядов и токов проводимости | |
| электромагнитного поля в отсутствие токов проводимости | |
| стационарных электрических и магнитных полей |
-----------------------------------------------------------------------
Решение:
Вторая система уравнений отличается от первой системы своими вторым и третьим уравнениями. Во втором уравнении иначе записано подынтегральное выражение, но  . В третьем уравнении отсутствует плотность
. В третьем уравнении отсутствует плотность 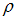 свободных зарядов. Следовательно, рассматриваемая система справедлива для электромагнитного поля в отсутствие свободных зарядов.
свободных зарядов. Следовательно, рассматриваемая система справедлива для электромагнитного поля в отсутствие свободных зарядов.
-----------------------------------------------------------------------
9. Утверждение «Переменное электрическое поле, наряду с электрическим током, является источником магнитного поля» раскрывает физический смысл уравнения …

| 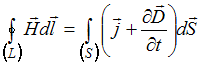
|

| |
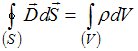
| |
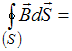 0. 0.
|
-----------------------------------------------------------------------
10. Обобщением теоремы Остроградского – Гаусса для электростатического поля в среде является уравнение …

| 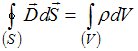
|
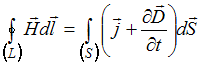
| |

| |

|
-----------------------------------------------------------------------
Решение:
Уравнение Максвелла 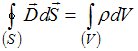 является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде – источником электрического поля являются свободные электрические заряды. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.
является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде – источником электрического поля являются свободные электрические заряды. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.
-----------------------------------------------------------------------
Дата добавления: 2015-02-16; просмотров: 893 | Поможем написать вашу работу | Нарушение авторских прав |