Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Полярные координаты

Введем в рассмотрение единичные векторы: , направленный по радиусу-вектору в сторону возрастания , и , повернутый относительно на угол в сторону возрастания угла (рис. 3.9). Единичные векторы и могут быть представлены через единичные векторы координатных осей:

,

.

Рис.3.9.

Рис. 3.10.

Производные по времени от единичных векторов , определяются соотношениями

, (3.12)

. (3.13)

Радиус-вектор , определяющий положение точки, может быть представлен в виде (рис. 3.9). При движении точки меняются как модуль, так и направление радиуса-вектора , следовательно, и , и являются функциями времени. На основании равенства (3.9) имеем

.

Используя соотношение (3.12), будем иметь

.

Полученная формула дает разложение вектора скорости на две взаимно перпендикулярные составляющие: радиальную и поперечную (рис. 3.10).

Проекции скорости на радиальное и поперечное направления

и 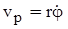(3.14)

называются соответственно радиальной и поперечной скоростями. Модуль скорости находится по формуле

. (3.15)

3.2.2. Скорость точки при естественном способе задания движения. Пусть точка М движется по какой-либо кривой (рис. 3.11). За промежуток времени 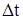точка переместится по кривой из положения М в положение М ₁. Дуга , если движение точки происходит в сторону положительного отсчета дуги (рис. 3.11 а), и , если движение происходит в противоположную сторону (рис. 3.11 б). На основании (3.9)
имеем .

Перепишем это равенство в виде

.

Так как предел отношения дуги к стягивающей ее хорде равен по модулю единице, а предельное положение секущей ММ ₁совпадает с направлением касательной к кривой в точке М, то

,

где 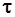– единичный вектор касательной к кривой, направленный в сторону положительного отсчета дуги.

Рис. 3.11.

Действительно, если , то вектор направлен в сторону (см. рис. 3.11 а), а при вектор направлен в сторону, противоположную (см. рис. 3.11 б). В обоих случаях этот вектор, а следовательно, и его предел , направлены в сторону возрастания дуги 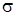(на рис. 3.11 положительное направление отсчета дуги 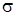выбрано вправо от начала отсчета М ₀).

Учитывая, что ,

имеем . (3.16)

Обозначая , получим

. (3.17)

Из формулы (3.17) следует, что . Очевидно, что , если движение происходит в сторону положительного отсчета дуги, и , если движение происходит в противоположную сторону.

Так как проходимый точкой путь всегда положителен, то элемент пути

и, следовательно, модуль скорости можно определить по формуле

.