Читайте также:
|
В последнее время активно развивается теория о нахождении кратчайших путей.
Пусть имеется граф G. Некоторая его вершина обозначена как вершина 1. Необходимо найти минимальные пути от вершины 1 до каждой из вершин графа. Минимальным путём будем называть путь с минимальной суммой цен вдоль пути. Ценой назовем неотрицательное число, являющееся весом ребра.
Существуют три наиболее эффективных алгоритма нахождения кратчайшего пути: алгоритм Дейкстры (используется для нахождения оптимального маршрута между двумя вершинами), алгоритм Флойда (для нахождения оптимального маршрута между всеми парами вершин) и алгоритм Йена (для нахождения k-оптимальных маршрутов между двумя вершинами)
Алгоритм Дейкстры
Идея основывается на следующем очевидном утверждении.
Пусть построен минимальный путь из вершины A в вершину B. И пусть вершина B связана с некоторым количеством вершин i. Обозначим через Ci – цену пути из вершины B в вершину i. Выберем из Ci минимальную величину. Тогда минимальное продолжение пути из точки B пойдёт через выбранную величину.
И из него вытекает следствие. Пусть есть множество вершин через которые уже проходят минимальные пути. Такое множество гарантированно есть, это вершина 1. Утверждение сформулированное выше даёт возможность добавлять к уже существующему множеству вершин (будем далее называть их выделенными) еще одну вершину, а так как в графе количество вершин конечно, то за конечное количество шагов все вершины графа окажутся выделенными, а это и будет решением.
Сущность алгоритма Дейкстры и заключается в процедуре добавления еще одной вершины к множеству выделенных. Эта процедура состоит из двух шагов:
1) Строим множество вершин инцидентных выделенным и находим среди их вершину с наименьшей ценой. Найденная вершина добавляется в множество выделенных.
2) Строим множество вершин инцидентных выделенным и определяем для них новые цены. Новая цена вершины это минимальная цена пути от множества выделенных вершин до данной вершины. Строится новая цена так:
a) Для невыделенной вершины во множестве выделенных определяется подмножество вершин инцидентных данной.
b) Для каждой вершины выделенной подмножества определяется цена пути до данной.
c) Определяется минимальная цена. Эта цена и становится ценой вершины.
Схема алгоритма:
1) Множество выделенных вершин = исходная вершина
2) Пока есть невыделенные вершины выполнять
a) Для каждой вершины инцидентной последней выделенной рассчитать предварительную цену как минимальную из уже имеющейся и цены, полученной с учетом пути от выделенной до данной.
b) Среди множества вершин, для которых определена предварительная цена, найти вершину с минимальным значением предварительной цены.
c) Найденную вершину занести во множество выделенных вершин.
Алгоритм Флойда
Пусть дан непустой взвешенный граф с произвольными весами ребер. Требуется найти кратчайшие длины путей между всеми парами вершин графа, если в графе нет циклов отрицательной длины или обнаружить наличие таких циклов.
Построим матрицу 
размерности |V| x |V|, элементы которой (обозначим из v) определяются по правилу:
= 0;
= Вес (
, 
), где i<>j, если в графе существует ребро (дуга) (, );
= бесконечность, где i<>j, если нет ребра (дуги) (, ).
Схема алгоритма:
1) Выполнять цикл, завершение которого наступает по выполнению одного из двух условий: либо количество шагов цикла равно V, либо был обнаружен цикл отрицательной длины. Шаги цикла нумеруются с нуля. Шаг цикла будем обозначать переменной m.
a) Строится матрица с индексом равным номеру шага, обозначим его через m, в которой элементы определяются через элементы матрицы предыдущего шага по следующим формулам:
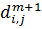+1=min{ 
, 
+ 
},
где i<>j; 
=0.
b) Если 
+ 
< 0 для какого-то i, то в графе существует цикл (контур) отрицательной длины, проходящий через вершину 
;
По завершению работы данного алгоритма, элементы матрицы равны длинам кратчайших путей между соответствующими вершинами.
Практическое применение алгоритмов решения задачи
Нахождение кратчайшего пути – жизненно необходимо и используется практически везде, начиная от нахождения оптимального маршрута между двумя объектами на местности (например, кратчайший путь от дома до университета), в системах автопилота, для нахождения оптимального маршрута при перевозках, коммутации информационного пакета в Internet и т.п.
Дата добавления: 2015-02-16; просмотров: 50 | Поможем написать вашу работу | Нарушение авторских прав |