Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Скаляры и векторы

Одиночные количественные характеристики и результаты измерений обычно формализуются понятием «скаляр» или «вещественное число». Иными словами, скалярная величина характеризуется только числом.

Формально вектор может быть определен как упорядоченный набор скаляров. Подобно тому, как вещественное число служит мерой отдельного свойства какого-либо объекта (скажем, диаметр электродвигателя), векторы используются для описания упорядоченных совокупностей свойств. Например, высота электрощита рассматривается как его первая характеристика, длина – как вторая, а ширина – как третья. Тогда электрощит, имеющий 500 мм высоты, 300 мм длины и 250 мм ширины может быть описан вектором.

Электрощит =

Векторные величины характеризуются не только числом, но и направлением. Направление, как правило, указывается стрелкой. На рис.1.1. изображен вектор АВ. Под численным значением или длиной вектора АВ понимается длина отрезка АВ, соединяющего начало А и конец В вектора АВ.

Рис.1.1. Двумерный вектор

Длину вектора часто называют модулем вектора и обозначают той же буквой, заключенной в вертикальные черты |x|, | АВ | или так: и . Вектор, определенный парой чисел, называется двумерным вектором. Геометрически двумерному вектору соответствует точка на плоскости. Аналогично вектор, определенный упорядоченной тройкой чисел (x_A, y_A, z_A), называется трехмерным вектором. Геометрически трехмерному вектору соответствует точка пространства (рис.1.2).

Рис.1.2. Трёхмерный вектор

Стандартная форма записи вектора опирается на привычный порядок чтения текстов сверху – вниз. Соответственно векторы изображаются вертикальными столбцами чисел с первой компонентой в верхней позиции. Вектор является вектором – столбцом в общем виде

=

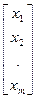
или n -мерным вектором. Числа x ₁, x ₂,..., x _n называют компонентами или координатами вектора . Последние, как правило, нумеруются индексом, пробегающим значения от 1 до n, где n – размерность вектора. Обозначением отдельной компоненты вектора будет служить его имя с нижним индексом, указывающим номер этой компоненты. Так, через x ₂, принято обозначать вторую компоненту вектора .

Если из вектора – столбца хотят получить вектор – строку, то эта операция называется транспонированием. В этом случае вектор – строка записывается в виде = (x ₁, x ₂,..., x _n)^T . Таким образом, если – вектор – столбец, тогда ^Т – вектор – строка, при этом ( ^Т)^Т – вновь вектор – столбец, причем =( ^T)^T.

Вектор, все компоненты которого равны нулю, называется нуль - вектором и обозначается 0 = (0, 0,..., 0) или 0 _n. В дальнейшем при обозначении векторов черту будем опускать.

Два вектора считаются одинаковыми, если их соответственные компоненты равны. Это определение предполагает, что проверяемые на совпадение вектора имеют одинаковую размерность, т.е. x_i = y_i, i =1, 2,..., n.

Суммой векторов x и y называют вектор, обозначаемый x+y, компоненты которого находят по формуле:

x+y = (x ₁+ y ₁, x ₂+ y ₂,..., x _n+ y _n). (1.1)

Разность векторов x и y определяют следующим образом:

х–y = (x ₁- y ₁, x ₂- y ₂,..., x _n- y _n). (1.2)

Произведением вектора x на вещественное число а называется вектор, обозначаемый а x, компоненты которого находят по формуле:

а x = (аx ₁, аx ₂,..., аx _n). (1.3)

Из приведенных определений непосредственно вытекает справедливость следующих равенств:

Коммутативность: x+y = y+x.

Ассоциативность: (x+y)+z = x+(y+z);

x+0_n = x;

0x=0_n;

a(x+y) = ax+ay;

(a₁+a₂)x = a₁x+a₂x.

Введем понятие скалярного произведения двух векторов. Если y – вектор строка размерности n, а x – вектор – столбец размерности n, то скалярное произведение двух векторов определяется равенством

или (1.4)

Например, y = (1, -2, 0)^T, х = ,<y,х> = 1∙2+(-2) 3+0∙1 = –4

Итак, чтобы получить скалярное произведение двух векторов надо перемножить соответствующие компоненты и результат сложить. Результат скалярного произведения – число.

Пример 1.1. Найти компоненты вектора: x= –2.5a+1.5b+c, если а = (2, 3, 4, 5)^Т, b = (1, 0, 2, 1)^T, c = (0, 4, 5, 1)^T.

Ответ: (-3.5, 11.5, -12, -12)^Т.

Пример 1.2. Сложить вектора: а) 3(1, -7, 5)^T-2(0, 2, -2)^Т+(-2, 26, -18)^Т =(1, 1, 1)^Т; б) (2, 1, -1, 3)^T+(1, -1, -2, 1)^T-(-4, 1, 5, -1)^T=(8, -2, -10, 2).

Среди скалярных произведений отметим x^Tx = <x, x > = .

Отметим свойства, которыми обладает скалярное произведение

1) <х, у> = <у, х>;

2) <х+у, z> = <x, z>+<y, z>;

3) < a x, y> = a <x, y>;

4) <x, x> > = 0 (равенство имеет место тогда и только тогда, когда х нулевой вектор 0_n).

Совокупность всех n -мерных векторов, для которых введены операции сложения, вычитания, умножения на вещественное число, а также скалярное произведение согласно формулам (1.1)…(1.4), называют n – мерным вещественным евклидовым пространством и обозначают Eⁿ. Для краткости это пространство будем называть просто евклидовым пространством.

Множество вещественных чисел далее будем обозначать E. Введем понятие – расширенная числовая прямая Ē=E U {-∞; +∞} (U – объединение). Множество E является примером одномерного евклидова пространства. Пространство E ² будем геометрически интерпретировать как совокупность точек плоскости с фиксированной прямоугольной системой координат или же, как совокупность векторов на этой плоскости, начало которых совпадает с началом прямоугольной системы координат. Пространство E ³ имеет аналогичную интерпретацию в пространстве трех измерений. Элементы пространства Eⁿ будем называть также точками.

Положительное значение квадратного корня х^Тх есть норма ||x|| или длина векторах Eⁿ (х принадлежит множеству Еⁿ), определяемая по формуле:

||x|| = (1.5)

Сформулируем основные свойства нормы вектора:

) ||x|| ≥ 0, причем ||x|| = 0 тогда и только тогда, когда х = 0_n;

) || a x|| = | a | ||x||, где а – число;

) ||x+y|| < = ||x|| +||y|| – неравенство треугольника;

) |<xy>| < = ||x||·||y|| – неравенство Коши – Буняковского.

Если норма определяется равенством (1.5), то всякое евклидово пространство становится нормированным. Полное евклидово пространство называется гильбертовым.

Расстояниемежду точками х и у евклидова пространства, обозначают через r(x, y) и определяют следующим образом:

r(х, у) = ||x-y|| = .