
Читайте также:
|
множество А содержится в множестве В или множество А является подмножеством множества В (в этом случае пишут А  В), если каждый элемент множества А одновременно является элементом множества В. Эта зависимость между множествами называется включением. Для любого множества А имеют место включения:
В), если каждый элемент множества А одновременно является элементом множества В. Эта зависимость между множествами называется включением. Для любого множества А имеют место включения: 
 А и А
А и А  А.
А.
4.
5. Прямым произведением или декартовым произведением  множеств
множеств  и
и  называется множество всех упорядоченных пар
называется множество всех упорядоченных пар  таких, что
таких, что  и
и  . При этом используют следующее обозначение:
. При этом используют следующее обозначение: 
6. Из каких элементов состоит множество действительных чисел?
Действительные числа, не являющиеся рациональными, называются иррационалъными. Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:
N={1; 2; 3;...; n;... } — множество натуральных чисел;
Zo={0; 1; 2;...; n;... } — множество целых неотрицательных чисел;
Z={0; ±1; ±2;...; ±n;...} — множество целых чисел;
Q={m/n: mÎZ,nÎN} — множество рациональных чисел.
R—множество действительных чисел.
Между этими множествами существует соотношение
NÌ ZoÌ ZÌ QÌ R.
Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, 1/2= 0,5 (= 0,500...), 1/3=0,333... — рациональные числа.
7. Числовая прямая - это множество действительных чисел.
Геометрической моделью числовой прямой служит координатная прямая.
8. Абсолю́тная величина́ или мо́дуль вещественного или комплексного числа x есть расстояние от x до начала координат.
Более точно:
Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:
- если x > 0, то | x | = x;
- если x <= 0, то | x | = − x.
Для любых  имеют место следующие соотношения:
имеют место следующие соотношения:
 (см. Функция sgn(x)).
(см. Функция sgn(x)).
 .
. Как для вещественных, так и для комплексных  имеют место соотношения:
имеют место соотношения:
 , причём | a | = 0 тогда и только тогда, когда
, причём | a | = 0 тогда и только тогда, когда  .
. .
. (неравенство треугольника).
(неравенство треугольника). .
. .
. .
. , если
, если  существует.
существует.9. Промежуток, или более точно, промежуток числовой прямой — множество вещественных чисел, обладающее тем свойством, что вместе с любыми двумя числами содержит любое, лежащее между ними.
Окрестностью точки  называется всякое открытое множество, содержащее эту точку. И, как следует из определения открытых множеств топологии τ, всякая окрестность точки a включает один из интервалов указанного вида, содержащий a.
называется всякое открытое множество, содержащее эту точку. И, как следует из определения открытых множеств топологии τ, всякая окрестность точки a включает один из интервалов указанного вида, содержащий a.
10. Выборка — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённойпроцедуры выбранных из генеральной совокупности для участия в исследовании.
Определение. Выборка называется упорядоченной, если в ней задан порядок следования элементов. Если порядок следования элементов несущественен, то выборка называется неупорядоченной.
11. Прямое или декартовое произведение двух множеств — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств.
14. Бином - иначе двучлен.
| При n =1 | (a + b)1= a + b, |
| При n =2 | (a + b)2= a 2+2 ab + b 2, |
| При n =3 | (a + b)3= a 3+3 a 2 b +3 ab 2+ b 3, |
| При n =4 | (a + b)4= a 4+4 a 3 b +6 a 2 b 2+4 ab 3+ b 4. |
Свойство коэффициэнтов бинома Ньютона
Формула бинома Ньютона позволяет доказать важную зависимость между биномиальными коэффициентами:
Cnm +1 = Cnm + Cnm +1.
15.
16. Разбие́ниемно́жества — это представление его в виде объединения произвольного количества попарно непересекающихся подмножеств. Семейство непустых множеств  , где A — некоторое множество индексов (конечное или бесконечное), называется разбиением X, если:
, где A — некоторое множество индексов (конечное или бесконечное), называется разбиением X, если:
1.  для любых
для любых  , таких что
, таких что  ;
;
2. 
17. Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс —интегрирование.
Пусть s = s (t) — закон прямолинейного движения. Тогда v (t 0) = s '(t 0) выражает мгновенную скорость движения в момент времени t 0. Вторая производная a (t 0) = s ''(t 0) выражает мгновенное ускорение в момент времени t 0.
18. Свойство дифференцируемости функции. Понятие дифференциала.
Линейную функцию  называют дифференциалом функции f в точке
называют дифференциалом функции f в точке  и обозначают df. Для функции x производная в каждой точке
и обозначают df. Для функции x производная в каждой точке  равна 1, то есть
равна 1, то есть  Поэтому пишут:
Поэтому пишут:
|
Приближенное значение функции вблизи точки  равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом:
равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом:

|
Свойство дифференцируемости функции
- Теорема 5.2 (Ролля) Пусть функция  дифференцируема на интервале
дифференцируема на интервале  , непрерывна в точках
, непрерывна в точках  и
и  и принимает в этих точках значение 0:
и принимает в этих точках значение 0:  . Тогда найдётся хотя бы одна точка
. Тогда найдётся хотя бы одна точка  , в которой
, в которой  .
.
- Теорема 5.3 (Лагранжа) Пусть функция  дифференцируема на интервале
дифференцируема на интервале  и непрерывна в точках
и непрерывна в точках  и
и  . Тогда найдётся такая точка
. Тогда найдётся такая точка  , что
, что

|
- Теорема 5.4 (Коши) Пусть функции  и
и  дифференцируемы на интервале
дифференцируемы на интервале  и непрерывны при
и непрерывны при  и
и  , причём
, причём  при всех
при всех  . Тогда в интервале
. Тогда в интервале  найдётся такая точка
найдётся такая точка  , что
, что

19. Правило дифференцирования суммы функций: 
Правило дифференцирования разности функций: 
Правило дифференцирования произведения функций (правило Лейбница): 
Правило дифференцирования частного функций: 
20. Правило дифференцирования сложной функции.Сложная функция (композиция функций, суперпозиция функций) обозначается  или
или  .
.
Производная композиции равна: 
Если необходимо взять производную от композиции трех и более функций, то последовательно применяем указанное выше правило. Например, 
Рассмотрим дифференциал функции в произвольной точке промежутка:. Здесь - приращение независимой переменной, которое является числом и не зависит от. Пусть теперь - функция независимого переменного, определенная на промежутке. Тогда - сложная функция переменного. Вычислим ее дифференциал, используя формулу для производной сложной функции:. Заметим, что и выражение для дифференциала принимает ту же форму, хотя здесь уже функция переменного. Это свойство дифференциала первого порядка называется инвариантностью (т.е. неизменностью) его формы. При вычислении дифференциала второго порядка придется учитывать, что - функция переменного. Поэтому и форма второго (а также и всех следующих) дифференциала неинвариантна.
21. Связь между производными взаимно-обратных функций. Записывают это так:
 или
или  ,
,
где индексы  и
и  показывают по какой переменной производится дифференцирование, т. е. какая из перемен принята за независимую.
показывают по какой переменной производится дифференцирование, т. е. какая из перемен принята за независимую.
Связь между производными взаимно обратных функций весьма наглядно иллюстрируется геометрически.
22. Производные основных элементарных функций. 
25. Формулу

задающую определение дифференциала, можно записать в виде приближённого равенства

если считать (при малых  ) значение бесконечно малой величины
) значение бесконечно малой величины  много меньшим, чем
много меньшим, чем  . Перенося
. Перенося  в правую часть, получаем:
в правую часть, получаем:

где  . С учётом выражения дифференциала через частные производные, находим, что
. С учётом выражения дифференциала через частные производные, находим, что

Эту формулу можно применять для приближённого вычисления значений функции  в точках
в точках  , если известны значения
, если известны значения  и её частных производных
и её частных производных  в точке
в точке  .
.
26. Производные и дифференциалы высших порядков и их вычисление.
27. ФЕРМА ТЕОРЕМА - утверждение теории чисел, согласно которому уравнение xn+yn=zn при n"2 не имеет целых положительных решений. Справедливость теоремы Ферма доказана для ряда показателей n, но в общем виде остается недоказанной. П. Ферма, высказавший эту теорему, не оставил ее доказательства. Вели́кая теоре́ма Ферма́ (или Последняя теорема Ферма) — одна из самых популярных теорем математики; её условие формулируется на понятийном уровне среднего общего образования, а доказательство теоремы искали многие математики более трёхсот лет. Окончательно доказана в 1995 году Эндрю Уайлсом.
Теорема утверждает, что:
Для любого натурального числа n > 2 уравнение  ,не имеет натуральных решений a, b и c.
,не имеет натуральных решений a, b и c.
32.
Функция f (x) называется возрастающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) < f (x2).
Функция f (x) называется убывающей на промежутке D, если для любых чисел x1 и x2 из промежутка D таких, что x1 < x2, выполняется неравенство f (x1) > f (x2).

Рисунок 1.3.5.1.
Промежутки возрастания и убывания функции.
На показанном на рисунке графике функция y = f (x),  возрастает на каждом из промежутков [a; x1) и (x2; b] и убывает на промежутке (x1; x2). Обратите внимание, что функция возрастает на каждом из промежутков [a; x1) и (x2; b], но не на объединении промежутков
возрастает на каждом из промежутков [a; x1) и (x2; b] и убывает на промежутке (x1; x2). Обратите внимание, что функция возрастает на каждом из промежутков [a; x1) и (x2; b], но не на объединении промежутков  Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.
Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.
Заметим, что если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.
Действительно, если x1 < x2 – корни этого уравнения на промежутке D (f(x)), то f (x1) = f (x2) = 0, что противоречит условию монотонности.
Перечислим свойства монотонных функций (предполагается, что все функции определены на некотором промежутке D).
-Сумма нескольких возрастающих функций является возрастающей функцией.
-Произведение неотрицательных возрастающих функций есть возрастающая функция.
-Если функция f возрастает, то функции cf (c > 0) и f + c также возрастают, а функция cf (c < 0) убывает. Здесь c – некоторая константа.
-Если функция f возрастает и сохраняет знак, то функция 1/f убывает.
-Если функция f возрастает и неотрицательна, то  где
где  , также возрастает.
, также возрастает.
Если функция f возрастает и n – нечетное число, то f n также возрастает.
-Композиция g (f (x)) возрастающих функций f и g также возрастает.
33. Когда мы дифференцируем функцию, каждой точке этой функции мы ставим в соответствие некоторое число – ее производную в данной точке. Таким образом, производная функции также является функцией.
Если функция  дифференцируема, то ее производную называют второй производной от f и обозначают
дифференцируема, то ее производную называют второй производной от f и обозначают  :
:

Вторая производная от параметрической функции x = x (t) и y = y (t) задается формулой:

Вторую производную иногда обозначают:  В физике вторую производную функции по времени нередко обозначают двумя точками:
В физике вторую производную функции по времени нередко обозначают двумя точками: 
Вторая производная определяет скорость изменения скорости или ускорение. Так, если x – координата материальной точки, движущейся со скоростью  то ускорение этой точки равно
то ускорение этой точки равно

Важным применением второй производной является анализ выпуклости функции.
Аналогичным образом задаются производные высших порядков. Если функция f (n –1) дифференцируема, то ее производную называют производной n -го порядка f (n) функции f.
Выпуклая функция — функция, у которой надграфик является выпуклым множеством. 
34. Экстремумы функций и их нахождение с помощью производных. Необходимый признак и достаточные признаки существования экстремума.
35. После того как мы обсудили многие аспекты поведения функции и способы их исследования, сформулируем общую схему исследования функции. Эта схема даст нам практический способ построения графика функции, отражающего основные черты её поведения.
Пусть дана функция  . Для её исследования нужно:
. Для её исследования нужно:
1). Найти её область определения  . Если это не слишком сложно, то полезно найти также область значений
. Если это не слишком сложно, то полезно найти также область значений  . (Однако, во многих случаях, вопрос нахождения
. (Однако, во многих случаях, вопрос нахождения  откладывается до нахождения экстремумов функции.)
откладывается до нахождения экстремумов функции.)
2). Выяснить общие свойства функции, которые помогут в определении её поведения: не является ли функция чётной либо нечётной (быть может, после сдвига влево или вправо по оси  ), не является ли она периодической.
), не является ли она периодической.
3). Выяснить, как ведёт себя функция при приближении аргумента  к граничным точкам области определения
к граничным точкам области определения  , если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.
, если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.
4). Если область определения  включает в себя лучи вида
включает в себя лучи вида  или
или  , то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при
, то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при  или
или  соответственно.
соответственно.
5). Найти точку пересечения графика с осью  (если
(если  ). Для этого нужно вычислить значение
). Для этого нужно вычислить значение 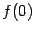 . Найти также точки пересечения графика с осью
. Найти также точки пересечения графика с осью  , для чего найти корни уравнения
, для чего найти корни уравнения  (или убедиться в отсутствии корней). Уравнение
(или убедиться в отсутствии корней). Уравнение  часто удаётся решить лишь приближённо, но уже отделение корней помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.
часто удаётся решить лишь приближённо, но уже отделение корней помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.
6). Найти интервалы монотонности функции  (то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной
(то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной  .
.
На стыках интервалов монотонности найти точки локального экстремума; вычислить значение функции в этих точках. Если функция имеет критические точки, не являющиеся точками локального экстремума, то полезно вычислить значение функции и в этих точках.
7). Найти интервалы выпуклости и вогнутости функции. Это делается с помощью исследования знака второй производной  . Найти точки перегиба на стыках интервалов выпуклости и вогнутости. Вычислить значение функции в точках перегиба. Если функция имеет другие точки непрерывности (кроме точек перегиба), в которых вторая производная равна 0 либо не существует, то в этих точках также полезно вычислить значение функции.
. Найти точки перегиба на стыках интервалов выпуклости и вогнутости. Вычислить значение функции в точках перегиба. Если функция имеет другие точки непрерывности (кроме точек перегиба), в которых вторая производная равна 0 либо не существует, то в этих точках также полезно вычислить значение функции.
8). В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой.
После выяснения свойств функции, упомянутых в пунктах 1 - 8, и нахождения опорных точек (точек пересечения с осями координат, точек графика, соответствующих точкам локального экстремума, точкам перегиба и проч.) мы можем достаточно точно построить график.
36. Нахождение наименьшего и наибольшего значений дифференцируемой функции на замкнутом интервале.
Модуль 2.
32. Дать определение базиса векторов а) на плоскости, б) в пространстве. Описать разложения вектора по базису. Базисом на плоскости называются два неколлинеарных вектора e1 e2 на этой плоскости, взятые в определённом порядке. Эти векторы e1 e2 называются базисными. Базисом в пространстве называются три некомпланарных вектора e1, e2, e3, взятые в определённом порядке. Эти векторы e1, e2, e3 называются базисными.
33. Дать понятие ортонормированного базиса и ориентации базиса. Как определяются прямоугольные координаты вектора? Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице. Аффинная система координат называется прямоугольной, если ее базис ортонормированный. Выбирая стандартные базисы, получаем: прямоугольную систему координат в пространстве — это точка О и три попарно перпендикулярных единичных вектора i, j, k (i- первый базисный вектор, j — второй, а k— третий; тройка векторов i,j, k— правая). Координаты векторов и точек в прямоугольной системе координат называются прямоугольными координатами. Координатами вектора в прямоугольной системе координат называются коэффициенты в разложении вектора по стандартному базису.
Дата добавления: 2015-02-16; просмотров: 26 | Поможем написать вашу работу | Нарушение авторских прав |