Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

МИНИМИЗАЦИЯ ПО ПРАВИЛЬНОМУ СИМПЛЕКСУ

ПРЯМЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ

Рассмотрим конкретные вычислительные алгоритмы решения задачи безусловной минимизации f (х) ® min, xÎ E _n, которые опираются только на вычисление значений функции f (х), т.е. прямые методы ми­нимизации. Важно отметить, что для их применения не требуется дифференцируемость целевой функции и даже ее аналитиче­ское задание. Нужно лишь иметь возможность вычислять или измерять значения f (х) в произвольных точках. Такие ситуации часто встречаются в практически важных задачах оптимизации.

Остановимся сначала на вычислительных процедурах вида (3.25), в которых выбор нового приближения к точке минимума определяется сравнением значений функции в нескольких точках пространства E _n.

МИНИМИЗАЦИЯ ПО ПРАВИЛЬНОМУ СИМПЛЕКСУ

Определение 3.7. Правильным симплексом в пространстве E _n на­зывается множество из п + 1 равноудаленных друг от друга точек (вер­шин симплекса). Отрезок, соединяющий две вершины, называется ребром симплекса.

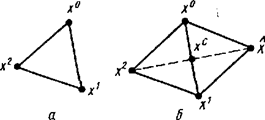
В пространстве E ₂ правильным симплексом является совокупность вершин равностороннего треугольника, в E ₃ – правильного тетраэдра.

Если х⁰ – одна из вершин правильного симплекса в E _n то координаты остальных п вершин х¹,..,х ⁿ можно найти, например, по формулам:

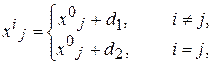(3.37)

где d ₁ 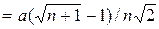, d ₂ , a– длина ребра. Вершину х⁰ симплекса, построенного по формулам (3.37), бу­дем называть бaзовой.

В алгоритме симплексного метода используется следующее важное свойство правильного симплекса. По известному симплексу можно построить новый симплекс отрaжением какой–либо вершины, например, х ^k симметрично относительно центра тяжести х ^c остальных вершин симплекса. Новая и старая вершины и х ^k связаны соотношением: , где x ^c . В результате получается новый правильный симплекс с тем же ребром и верши­нами = 2x ^c – х ^k, х ⁱ, i = 0,.., n, i¹ k. Таким образом, происходит перемещение симплекса в пространстве Е _n. На рис. 3.3 представле­на иллюстрация этого свойства симплекса в пространстве Е ₂.

Поиск точки минимума функции f (x) с помощью правильных сим­плексов производят следующим образом. На каждой итерации срав­ниваются значения f (х) в вершинах симплекса. Затем проводят опи­санную выше процедуру отражения для той вершины, в которой f (х) принимает наибольшее значение. Если в отраженной вершине получа­ется меньшее значение функции, то переходят к новому симплексу. В противном случае выполняют еще одну попытку отражения для вер­шины со следующим по величине значением f (х). Если и она не при­водит к уменьшению функции, то сокращают длину ребра симплекса, например, вдвое и строят новый симплекс с этим ребром. В качестве базовой выбирают ту вершину х⁰ старого симплекса, в которой функция принимает минимальное значение. Поиск точки минимума f (x) заканчивают, когда либо ребро симплекса, либо разность между значе­нии функции в вершинах симплекса становятся достаточно малыми. Опишем один из вариантов алгоритма этого метода.

Шаг 0. Выбрать параметр точности e, базовую точку х⁰, ребро a и построить начальный симплекс по формулам (3.37). Вычислить f (х⁰).

Шаг 1. Вычислить значения f (х) в вершинах симплекса х¹,.., x ⁿ.

Шаг 2. Упорядочить вершины симплекса х⁰,.., х ⁿ так, что бы f (х⁰) £ …£ £ f (х¹) £ f (х ^{n –1}) £ f (х ⁿ).

Шаг 3. Проверить условие

(3.38)

Если оно выполнено, то вычисления прекратить, полагая х^*» х⁰, f ^*» f (x⁰).

В противном случае перейти к шагу 4.

Шаг 4. Найти и выполнить отражение вершины х ⁿ:

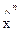= 2x ^c – х ⁿ. Если f () <f ( x ⁿ), то положить х ⁿ = и перейти к шагу 2. Иначе – перейти к шагу 5.

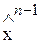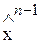Шаг 5. Найти и выполнить отражение вершины х ^{n– 1}: = 2x ^c – х ^{n– 1}. Если f () < f (х ^{n– 1}), то положить х ^{n– 1} = и перейти к шагу 2. Иначе – перейти к шагу 6.

Шаг 6. Перейти к новому правильному симплексу с вдвое меньшим ребром, считая базовой вершиной х⁰. Остальные п вершин симплекса найти по формуле х ⁱ = (х ⁱ + х⁰)/2, i= 1, .., п. Перейти к шагу 1.

Геометрическая иллюстрация работы алгоритма в пространстве показана на рис. 3.4, где точки х ⁰, х ¹, х ² – вершины начального симплекса, а пунктиром указаны процедуры отражения.

Замечания:

1. Следует иметь в виду, что если функция f (х) многомо­дальна, то описанным методом может быть найдена точка ло­кального, а не глобального минимума f (х).

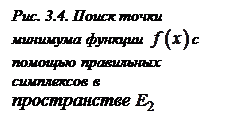2. Если ограниченность снизу целевой функции не оче­видна, то в алгоритм метода следует включить дополни­тельную процедуру останова.