Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Полные системы. Теорема Поста

Система булевых функций называется полной, если любая булева функция может быть выражена через функции этой системы с помощью суперпозиций.

Теорема (Поста о полноте). Класс функций K полон тогда и только тогда, когда он не содержится целиком ни в одном из классов P ₀, P ₁, S, L, M.

Примеры

1. Доказать, полноту системы функций а) {Ù,’}, б) {¯}.

Решение. а) Система функций {Ù, Ú, ’} полна, поскольку любая функция представима в СДНФ (СКНФ), т.е. выражается через дизъюнкцию, конъюнкцию и отрицание. Выразим дизъюнкцию через конъюнкцию и отрицание: x Ú y =(x ’ y ’)’. Следовательно, любую функцию можно выразить и через конъюнкцию и отрицание, откуда следует полнота.

б) Выберем какую-либо полную систему функций, например, из предыдущего пункта {Ù,’}. Выразим входящие в систему функции через стрелку Пирса:

x ’= x ¯ x, xy = x ’¯ y ’=(x ¯ x)¯(y ¯ y).

Здесь мы использовали формулы (1) – (2) из §5.1.

2. Доказать, что система функций {Ù,Å} не полна, а система {Ù,Å, 1} – полна.

Решение. Составим таблицу принадлежности функций к классам P ₀, P ₁, S, L, M («+» означает принадлежность, «–» - нет):

Первые две строки соответствуют системе {Ù,Å}. Согласно теореме Поста, полная система функций не должна содержаться целиком ни в одном классе, но функции Ù и Å обе содержатся в классе P ₀. Следовательно, система функций {Ù,Å} неполна.

При рассмотрении всех строк (система {Ù,Å,1}), обнаруживаем, что каждый столбец содержит хотя бы один минус, следовательно, данная система полна.

3. Записать функцию f = x Ú y, используя стрелку Пирса ¯.

Решение. Разложим функцию f по системе {Ù, ’}, а затем по системе {¯}, используя (1), (2):

{Ù, ’}: f = x Ú y =(x ’ y ’)’

{¯}: f =((x ¯ x)(y ¯ y))’=((x ¯ x)(y ¯ y))¯((x ¯ x)(y ¯ y))=

={[(x ¯ x)¯(x ¯ x)]¯[(y ¯ y)¯(y ¯ y)]}¯{[(x ¯ x)¯(x ¯ x)]¯[(y ¯ y)¯(y ¯ y)].

4. Представить штрих Шеффера в виде полинома Жегалкина.

Решение. Требуется разложить функцию f = x ½ y по системе функций {Ù,Å,1}. Разложим функцию f по системе {Ù, ’}, затем по системе {Ù,Å,1}, используя (1),(3):

{Ù, ’}: f = x ½ y = x ’Ú y ’=(xy)’,

{Ù,Å,1}: f =1Å xy.

Вопросы и упражнения для самостоятельной работы

14. Доказать полноту следующих систем функций двумя способами (исходя из определения и используя теорему Поста)

а) {½}; б) {1, ®}; в) {Ú,’}.

15. Проверить полноту системы функций

а) {0, Å}; б) {0, ®}; в) {Ú,«}; г) {®,1, Ú}.

16. Доказать, что существует ровно две полные системы функций двух переменных, каждая из которых состоит из одной функции.

17. Разложить функции f и g по указанной системе функций:

а) f =(x ’¯ y)½ z, g =(x Å y ’)¯ z ’ по {Ú, ‘};

б) f = x «y ’, g =(x ’Ú y) z по {Ù,Å,1};

в) f = x Ú y, g = x ’ y по {1, ®}.

18. Записать функцию 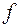, используя штрих Шеффера ½:

а) f = xy; б) f = x ¯ y; в) f = x ® y ’ z.