Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Метод бисекции

Лабораторная работа №3

Решение нелинейных уравнений

Теория

Метод бисекции

Пусть необходимо решить уравнение , где 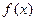непрерывна на отрезке [a;b] и корень 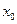заключен в том же интервале т.е.

Разделим отрезок [a;b] пополам, т.е. найдем 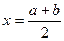и вычислим значение функции 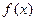в этой точке.

Если окажется, что , то х–корень уравнения. Если же 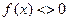, то выбираем ту половину отрезка [a;х] или [х;b], на концах которой функция 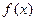имеет противоположные знаки. Это отрезок [х;b]. Половина участка, не содержащая корня ([a;х]), отбрасывается, и левая граница интервала перемещается в точку деления пополам (а = х).

При повторном делении производятся те же самые операции: новый отрезок [a;b] делится пополам, вычисляется значение функции в точке деления 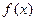и определяется отрезок, содержащий истинный корень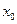

Процесс деления продолжают до тех пор пока длина отрезка [a;b], содержащего корень, не будет меньше некоторого наперед заданного е. И пока значение функции в точке деления 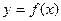превышает по абсолютной величине е.

Метод касательных

Пусть уравнение имеет один корень на отрезке [a;b], а его первая и вторая производные определены, непрерывны и сохраняют постоянные знаки в этом интервале.

Геометрически, метод Ньютона эквивалентен замене небольшой дуги кривой 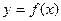касательной в некоторой точке кривой.

Выберем в качестве первого приближенного значения корня точку 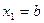, для которой выполняется условие 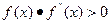, т.е. значения функции и ее второй производной в точке х имеют одинаковые знаки. Напомним, что знак второй производной от функции 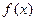определяет выпуклость кривой: если 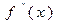положительна, то график функции имеет выпуклость вниз.

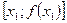Через точку с координатами проведем касательную к кривой 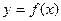. В качестве второго приближения 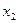корня возьмем абсциссу точки пересечения этой касательной с осью Ох. Через точку 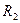снова проведем касательную, абсцисса точки пересечения которой даст нам следующее приближение 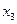корня и т.д.

Уравнение касательной, проходящей через точку , имеет вид:

Полагая у=0, а х= 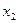, найдем абсциссу 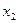точки пересечения касательной с осью Ох:

Следующее приближение 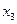находим по формуле:

Применяя формулы уточнения значения корня многократно, получим в общем виде:

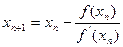
Процесс вычислений заканчивают обычно по условию

Разность между соседними приближениями должна быть меньше заданной степени точности е.

Задание:

Решить уравнение методом бисекции и касательных

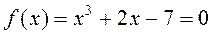(вар. 11)

Программный код:

unit lab6;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, jpeg, ExtCtrls, Grids;

type

TForm1 = class(TForm)

GroupBox1: TGroupBox;

Image1: TImage;

GroupBox2: TGroupBox;

Button1: TButton;

Button2: TButton;

Button3: TButton;

GroupBox3: TGroupBox;

x1: TEdit;

x2: TEdit;

eps: TEdit;

GroupBox4: TGroupBox;

result: TStringGrid;

procedure Button1Click(Sender: TObject);

procedure FormCreate(Sender: TObject);

procedure Button2Click(Sender: TObject);

procedure Button3Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

epsilon: real;

implementation

{$R *.dfm}

procedure inicial(); //заполнение

begin

form1.x1.Text:='1,2';

form1.x2.text:='1,5';

form1.eps.text:='0,001';

form1.result.cells[0,0]:='Метод';

form1.result.cells[1,0]:='x';

form1.result.cells[0,1]:='Бисекции';

form1.result.cells[0,2]:='Касательных';

form1.result.cells[2,0]:='Проверка';

form1.result.cells[2,1]:='не проверено';

form1.result.cells[2,2]:='не проверено';

end;

function fx(x:extended):extended; // F(x)

begin

fx:=(sqr(x)*x)+2*x-7;

end;

function f1x(x:extended):extended; // F`(x)

begin

f1x:=(3*sqr(x))+2;

end;

procedure TForm1.Button1Click(Sender: TObject);

begin

close;

end;

procedure TForm1.FormCreate(Sender: TObject);

begin

inicial();

end;

procedure TForm1.Button2Click(Sender: TObject);

var

l_kr, p_kr: extended; //левый и правый края итераций

res: extended; //x

fox: extended; //F(x)

begin

epsilon:=strtofloat(eps.text);

l_kr:=strtofloat(x1.Text);

p_kr:=strtofloat(x2.Text);

res:=(l_kr+p_kr)/2;

fox:=fx(res);

while fox>=epsilon do

begin

res:=(l_kr+p_kr)/2;

fox:=fx(res);

if fox>0 then

begin

p_kr:=res;

end

else

begin

l_kr:=res;

end;

end;

form1.result.cells[1,1]:=floattostr(res);

if fox<epsilon then

form1.result.cells[2,1]:='проверено';

end;

procedure TForm1.Button3Click(Sender: TObject);

var

xn, xnp1:extended;

xnt, xnp1t:extended;

begin

epsilon:=strtofloat(eps.text);

xn:=strtofloat(x2.Text);

xnp1:=xn-(fx(xn)/f1x(xn));

while abs(xnp1-xn)>=epsilon do

begin

xn:=xnp1;

xnp1:=xn-(fx(xn)/f1x(xn));

end;

form1.result.cells[1,2]:=floattostr(xnp1);

if abs(xnp1-xn)<epsilon then

form1.result.cells[2,2]:='проверено';

end;

end.