Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Ознайомлення з дробами

ПЛАН

Ознайомлення з частками

2. Розв’язування задач на знаходження частки числа і числа за його часткою

Ознайомлення з дробами

ЛІТЕРАТУРА

1. Богданович М. В., Козак М. В., Король Я. А. Методика викладання математики в початкових класах: Навчальний посібник для студентів педагогічних навчальних закладів. — Тернопіль: Навчальна книга – Богдан, 2006. — 336 с.

2. Богданович М.В. Методика розв’язування задач у початковій школі. – К.: Вища школа, 1990. – 183 с.

3. Богданович М. В., Будна Н.О., Лишенко Г.П. Урок математики в початковій школі. Навчальний посібник. - Тернопіль. Навчальна книга - Богдан. 2004. - 208с.

4. Король Я. А. Математика в початкових класах. Культура усного і писемного мовлення. — Тернопіль: Навчальна книга – Богдан, 2000. — 160с.

5. Король Я. А. Практикум з методики викладання математики в початкових класах: Навчальний посібник для педагогічних університетів та інститутів. – Тернопіль: Мандрівець, 1998, - 134 с.

6. Корчевська О. П. Робота над завданнями підвищеної складності з математики в початкових класах. — Тернопіль: Підручники і посібники, 2001. — 112 с.

Відповідно до програми з математики в початкових класах учнів треба підготувати до вивчення дробів у V класі. Це означає, що в початкових класах треба створити конкретні уяв­лення про частку і дріб. Для цього в IIІ класі ознайомлюють дітей з частками, записом їх, навчають порівнювати частки, розв'язува­ти задачі на знаходження частки числа і числа за часткою; у IV класі ознайомлюють з дробами, записом їх, навчають порівнюва­ти дроби, розв'язувати задачі на знаходження дробу від числа. Усі ці питання розкривають за допомогою наочності

1. Ознайомлення з частками

Ознайомити дітей з частками означає сформувати в них кон­кретні уявлення про частки, тобто навчити дітей утворювати част­ки практично. Наприклад, щоб дістати одну четверту частку кру­га, треба круг поділити на чотири рівні частини і взяти одну таку частину. Щоб дістати одну п'яту частку відрізка, треба поділити його на п'ять рівних частин і взяти одну таку частину.

Щоб сформувати правильні уявлення про частки, треба викори­стати достатню кількість різних наочних посібників. Як показав досвід, найзручнішими посібниками є геометричні фігури, виріза­ні з паперу; можна використати рисунки фігур, виконані на па­пері або в діапозитивах (круги, прямокутники, трикутники, брус­ки, відрізки тощо). Дуже важливо, щоб посібники були не тільки в учителя, а й у кожного учня. Правильні уявлення про частки, а пізніше про дроби будуть сформовані тоді, коли учні своїми руками зроблять, наприклад, половину круга, квадрата тощо, чверть відрізка і т. д.

Покажемо, як можна ознайомити дітей з частками.

У кожного з учнів і в учителя є по кілька однакових кругів, прямокутників (квадратів).

Візьміть два однакові круги. Один з них поділіть на дві рівні частини (показує, як треба перегнути і як розрізати круг). Це один круг, а це — половина круга, інакше кажучи, одна друга частка круга. Скільки других часток у цілому крузі? (2). Покажіть їх. Візьміть квадрат.

Як дістати одну другу частку, чи половину квадрата? (Поділити його на дві рівні части­ни і взяти одну таку частину). Виконуйте.

Учні можуть це зробити різними способами, наприклад: роз­різати квадрат по діагоналі і дістати два рівні трикутники або розрізати квадрат по середній лінії, тоді утвориться два прямо­кутники. Деякі учні можуть запропонувати й інші способи поділу квадрата на дві рівні частини. Як дістали одну другу частку круга? (Поділили круг на дві рівні частини і взяли одну таку частину.) Як дістали одну другу частку квадрата? Як інакше називають одну другу частку круга, квадрата? (Половина круга, половина квадрата). Скільки поло­вин круга в цьому крузі? (2.)

Учні накладають половини круга на цілий круг.

Частки записують за допомогою двох чисел. Одну другу част­ку круга, квадрата позначають так: 1/2

Число 2 показує, що круг, квадрат або іншу фігуру (чи предмет) поділено на 2 рівні частини, а число 1 показує, що взяли одну таку частину.)

Учні записують на половинах круга « 1/2 » і пояснюють, що показує в цьому записі кожне число. Так само утворюють частки:

1/4, 1/8, 1/3 та ін..

При цьому учні повинні усвідомити, що для того, щоб дістати, наприклад, 1/5 відрізка (прямокутника, паперової смужки тощо), треба цей відрізок (прямокутник, смужку) поділити на 5 рівних ча­стин і взяти одну таку частину; що в цьому відрізку (прямокутнику,

смужці) 5 п'ятих часток; що одну п'яту частку записують так: 1/5;

що в цьому записі число 5 означає, на скільки рівних частин поді­лили відрізок (прямокутник, смужку,), а число 1 показує, що взято одну таку частку. Для закріплення цих знань і умінь учням пропо­нують різні вправи.

Це насамперед вправи на називання і записування часток. Назвіть і запищіть, яку частку квадрата (круга) відрізано (розмальовано, заштриховано).

Можна запропонувати самим дітям зобразити яку-небудь частку відрізка (круга, квадрата і т. д.) і записати цю частку.

У кожному випадку треба записувати, скільки всього часток у цілому. Наприклад, скільки четвертих часток круга у цілому кру­зі? Скільки третіх часток відрізка в усьому відрізку?

Ефективною вправою для формування уявлень про частки є практичне порівняння часток тієї самої величини за допомогою на­очних посібників.

Наприклад, пропонують порівняти частки 1/3 і 1/2 і поставити знак «>» або «<».

Учні зображують частки, наприклад, за допомогою відрізків.

• • • • • • •

1/3 1/2

Порівнюють їх і переконуються, що 1/3 менше, ніж 1/2.

2. Розв’язування задач на знаходження частки числа і числа за його часткою

Розв'язування задач на знаходження частки числа і числа за його часткою також сприяє формуванню уяв­лень про частки величини. У цьому їх основне призначення. Тому задачі на знаходження частки числа і числа за його часткою роз­в'язують.на наочній основі.

Розглянемо, як можна ознайомити учнів з розв'язуванням задач кожного виду.

Спочатку вводять задачі на знаходження частки числа. Для ознайомлення з розв'язуванням задач краще пропонувати задачі, які легко ілюструвати. Наприклад, пропонують задачу: «Від смужки довжиною 15 см відрізали — її. Чому дорівнює довжина відрізаної смужки?» Учні відрізують смужку 15 см завдовжки. Потім з'ясовують, як знайти одну третю частину смужки (поділити її на З рівні частини і взяти одну таку частину). Учні практично ділять смужку (перегинають її), а потім відрізують одну третю частину. Розв'язання записують так:

15: 3=5 (см.). Відповідь: 5 см.

Під час.розв'язання інших задач досить скористатись креслен­ням: число зобразити відрізком, який-учні ділять на задане число рівних частин, позначають частку, після чого розв'язують усно або письмово.

Потім дають задачі на знаходження частки числа для усної та письмової роботи. Треба більше давати завдань виду: скільки сантиметрів у 1/2 м,? Скільки хвилин в 1/2 годині; в 1/5 годині?

Вивчаючи тему «Час», треба пояснити дітям, чому кажуть: «по­ловина на другу», «без чверті 10» і т. д.

Задачі на знаходження числа за його част­кою спочатку треба брати такі, щоб їх можна було безпосередньо ілюструвати, наприклад: «Сергійко відрізав від дротини 4 см. Це 1/3 всієї дротини. Яка довжина дротини?»

Зобразимо кусок дротини, який відрізав Сергійко. (Креслять відрізок 4 см завдовжки.) Яку частину всієї дротини становить від­різаний кусок? (1/3). Як зобразити всю дротину? (Взяти 3 рази по 4 см.) Чому? (4 см — це 1/3 дротини, а в усій дротині буде три треті.) Накресліть. (Виконують.) Якої довжини була дротина? (12 см.). Як дізнатися? (4-3.)

Запис розв'язання: 4∙3=12. Відповідь: 12 см.

Для задачі на знаходження числа за його часткою і задачі на знаходження частки числа вводять по черзі і пропонують як для усного, так і для письмового розв'язування. Зазначимо, що краще розв'язувати задачі з конкретним змістом, а не з абстрактними числами (щоб учні конкретно уявляли частку величини (одну тре­тину відра води, чверть кошика яблук, одну п'яту частину сувою тканини, одну соту частину метра тощо).

У IIІ класі розглядають лише прості задачі на знаходження част­ки і числа за його часткою, а в IV класі ці задачі включають до складених.

3. Ознайомлення з дробами

Утворення дробів, як і утворення часток, розглядають за допо­могою наочних посібників.

Поділіть круг на 4 рівні частини. Як назвати кожну таку части­ну? Запишіть. Покажіть три четверті частки. Ви дістали дріб — три четверті. Хто зможе записати цей дріб? Що показує число 4? (На скільки рівних частин поділили круг). Що показує число З? (Скільки таких частин узяли). Аналогічно учні дістають і запису­ють інші дроби, пояснюючи, що показує кожне число.

Для закріплення здобутих знань розв'язують такі самі вправи, як і під час ознайомлення з частками: за ілюстраціями, нази­вають і записують, які дроби зображені, або зображують дріб за допомогою креслення, рисунка. Засвоєнню конкретного змісту дро­бу допомагають вправи на порівняння дробів, а також розв'язуван­ня задач на знаходження дробу числа.

Для порівняння дробів звичайно використовують ілюстрації з однаковими прямокутниками.

Учням пропонують накрес­лити в зошиті прямокутник, довжина якого 16 см, а ширина 1 см. Це один прямокутник. Запишемо. (У першому прямокутнику запи­сують число 1.) Накресліть під першим прямокутником такий самий другий і поділіть його на 2 рівні частини. (Виконують.) Які частки дістали? (Другі, половини). Скільки других часток у цілому прямокутнику? Підпишіть. Нижче Накресліть такий самий прямо­кутник і поділіть його на 4 рівні частини. Як називається кожна частина? Скільки четвертих часток у цілому прямокутнику? Скіль­ки четвертих часток у половині? Що більше: одна друга чи одна четверта; одна друга чи дві четверті; одна четверта чи три четверті; дві другі чи чотири четверті? Накресліть четвертий такий самий прямокутник і поділіть його на 8 рівних частин. Як називаються утворені частки? Скільки восьмих часток у цілому? Скільки вось­мих часток в одній чверті; у половині прямокутника? Що більше: три восьмих чи одна четверта? Якому дробу дорівнює одна друга?

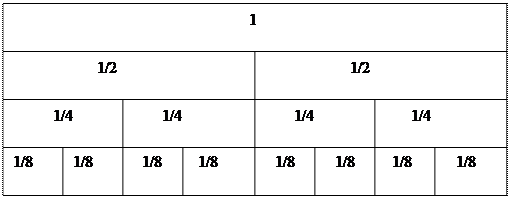Відповіді на всі такі запитання діти дають, користуючись, рисунком: порівнюючи, наприклад, 3/8 і 1/4, вони з рисунка бачать, що 3/8 більше, ніж 1/4 того самого прямокутника. Таким самим способом порівнюють і інші дроби, але для порівняння їх викорис­товують інші ілюстрації: наприклад, для порівняння дробів із зна­менниками 3, 6 і 9 однакові прямокутники ділять відповідно на З, 6 і 9 рівних частин, а для порівняння дробів із знаменниками 2, 5 і 10 однакові прямокутники ділять відповідно на 2, 5 і 10 рівних частин.

Пропонують спеціальні вправи на порівняння дробів:

1) Вставте пропущений знак «>», «<» або «=»:

3/8 * 3/4; 4/5 * 1; 4/8 * 1/2

2) Доберіть таке число, щоб рівність (нерівність) була пра­вильна:

5/10 = /2; 3/8 > /4; 1/2 < /4

Виконуючи такі вправи, учні використовують відповідні ілюст­рації з прямокутниками або заново зображують дроби за допомо гою, наприклад, відрізків. Так, порівнюючи дроби 3/8 і 3/4 учень

виконує рисунок і міркує так: «Зображує на відрізку дріб —; для цього відрізок поділю на 8 рівних частин і візьму 3 таких частини; зображу на такому самому відрізку дріб 3/4; поді­лю відрізок на 4 рівні частини і візьму 3 такі частини; відразу видно, що 3/4 відрізка більше, ніж 3/8 його. Запишу: 3/4 > 3/8»

Конкретний зміст дробу дуже яскраво розкривається під час розв'язування задач на знаходження дробу числа. Ці задачі, як і задачі на знаходження частки числа, розв'язують за допомогою від­повідних наочних посібників.

Наприклад, пропонують задачу. «У монтера було 12 м проводу. 2/3 всього проводу він витратив. Скільки метрів проводу витратив монтер?»

Учні під керівництвом учителя виконують рисунок.

Зобразимо відрізком кусок проводу, взявши 1 см за 1 м. Якої довжини відрізок треба накреслити? (12 см.) Що сказано про витрачений провід? (Витрачено 2/3 всього проводу). Як зобразити витрачений кусок проводу? (Відрізок поділити на 3 рівні частини і взяти 2 такі частини). Отже, спочатку 12 поділимо на 3. Про що дізнаємось? (Чому дорівнює 1/3 проводу). Чому ж вона дорівнює? (4 м.) Потім результат помножимо на 2. Про що дізнаємося? (Чому дорівнює 2/3 проводу). Скільки ж метрів проводу витратив монтер? (8м.)

Запис: 12:3∙2 = 8м. Відповідь: 8м.

Пізніше, розв'язуючи такі задачі, учні повинні самостійно міркувати. Наприклад, треба визначити, скільки хвилин у 3/4 год. Учень міркує: «Знайду, скільки хвилин становить 1/4 год, для цього 60 поділю на 4, буде 15; тепер знайду, скільки хвилин у 3/4 год, для цього 15 помножу на 3, буде 45 отже, 3/4 год — це 45 хв».

Задачі на знаходження дробу числа треба пропонувати як для усного, так і для письмового розв'язування.

Трохи пізніше задачі на знаходження дробу числа треба вклю­чити до складених задач, наприклад: «Мотоцикліст проїхав за 3 дні 1250 км. За перший день він проїхав 2/5 всього шляху, а за другий — 3/10 усього шляху. Яку відстань проїхав мотоцикліст за третій день?»

Записувати розв'язання таких задач краще у вигляді окремих

дій:

1) 1250: 5∙2=500 (км)—проїхав мотоцикліст першого дня;

2) 1250:10∙3=375 (км) — проїхав мотоцикліст другого дня;

3) 500+375 = 875 (км) —• проїхав мотоцикліст за 2 дні;

4) 1250 — 875=375 (км)—проїхав мотоцикліст третього дня.

Відповідь: 375 км.

Різні вправи з дробами слід частіше включати" для усних і пись­мових робіт протягом усього навчального року.