Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Линеаризация уравнений

Многие механические и электрические элементы в достаточно широком диапазоне изменения переменных можно считать линейными. Этого нельзя сказать о тепловых и гидравлических элементах, которые чаще всего по принципу своего действия оказывают­ся нелинейными.

Конечной целью моделирования динамики процессов является использование моделей в системах управления для определения динамических характеристик, следовательно, любым способом надо найти решение уравнений. Поэтому дифференциальные и разностные уравнения, образующие математическую модель объекта управления, выводятся на основе различных упрощающих предположений. Линейные дифференциальные уравнения решаются сравнительно легко. Однако не всегда возможно описать поведение объекта линейным уравнением. Поэтому применяется аппроксимация нелинейных связей в заданном диапазоне аргументов линейными соотношениями. Другими словами, в заданном диапазоне входных аргументов нелинейные уравнения заменяются линейными – линеаризуются. В линейных объектах связи входных и выходных сигналов легко описываются с помощью передаточной функции. Такая идеализация значительно упрощает процесс построения модели. Например, линеаризация дифференциальных и разностных уравнений приводит к линейным динамическим моделям, математический аппарат которых разработан наиболее полно. В результате решения таких уравнений получаются характеристики переходного процесса, зависящие от времени и параметров объекта.

Нелинейные элементы часто удается линеаризовать при условии малых отклонений сигналов от их стационарных значений.

Пусть некоторый элемент характеризуется входными величинами , выходной y(t) и внешним воздействием f(t). Динамическое уравнение элемента имеет произвольный нелинейный вид:

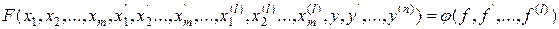(1.5.4)

Допустим, что установившийся процесс имеет место при некоторых постоянных Тогда уравнение установившегося состояния согласно (1.5.4) будет

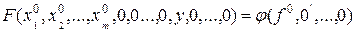(1.5.5)

В основе линеаризации нелинейных уравнений лежит предположение о том, что в исследуемом динамическом процессе переменные изменяются так, что их отклонения от установившихся значений 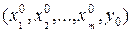остаются все время достаточно малыми (см.рисунок).

Обозначим указанные отклонения через 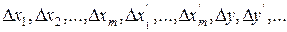Тогда в динамическом процессе

Условие достаточной малости динамических отклонений переменных от некоторых установившихся значений для системы автоматического регулирования обычно выполняется. Этого требует сама идея работы замкнутой автоматической системы.

Внешнее воздействие f(t) не зависит от работы автоматической системы, изменение его может быть произвольным, и поэтому правая часть уравнения (1.5.4) обычно линеаризации не подлежит (в отдельных случаях ее тоже можно линеаризовать).

Линеаризация обычно проводится путем разложения нелинейных зависимостей в ряд Тейлора в окрестности исходного стационарного режима с сохранением только линейных частей разложения и последующим вычитанием уравнений статики. С помощью этой процедуры получаются уравнения модели не относительно ее переменных, а отклонений переменных от исходного стационарного режима. Такое преобразование дает возможность легко применить преобразования Лапласа для записи модели объекта в виде передаточных функций.

Разложим функцию F в ряд по степеням указанных выше малых отклонений, рассматривая все производные как самостоятельные переменные (ряд Тейлора) и запишем уравнение (1.5.4) в следующем виде:

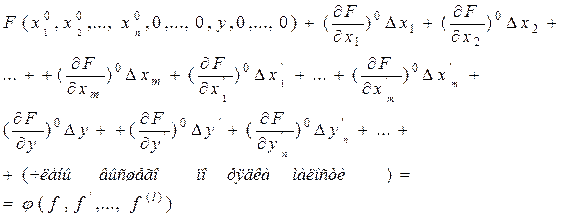(1.5.6)

Здесь частные производные с индексом «0» обозначают значение соответствующих производных в точке установившегося состояния. То есть в полученном уравнении все частные производные будут некоторыми постоянными коэффициентами (они будут переменными во времени, если функция F содержит t в явном виде или если установившийся процесс определяется переменными значениями).

Члены высшего порядка малости в уравнении (1.5.6) состоят из произведений и степеней малых отклонений с коэффициентами в виде смешанных частных производных и частных производных второго и высших порядков от функции F по всем переменным.

Вычтя из уравнения (1.5.6) почленно уравнение установившегося состояния (1.5.5) и отбросив члены высшего порядка малости, получим искомое линеаризованное уравнение динамики в виде

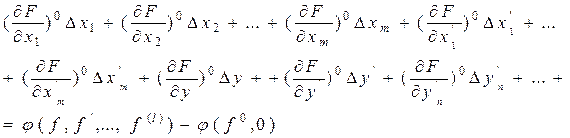(1.5.7)

Это дтфференциальное уравнение, также как и уравнение (1.5.4), описывает тот же динамический процесс. Отличие этого уравнения от первоначального в следующем:

- неизвестными функциями времени в этом уравнении являются не прежние величины 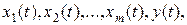а их отклонения от некоторых установившихся значений ;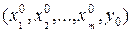

- полученное уравнение является линейным относительно отклонений переменных ;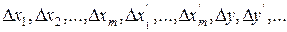

- это уравнение является более приближенным, так как в процессе его вывода были отброшены малые высшего порядка

Уравнение (1.5.7) называется дифференциальным уравнением в отклонениях.

Рассмотрим геометрическую трактовку процедуры линеаризации на примере элемента с одни входом x(t) и одним выходом y(t). Связь между переменными определяется уравнением

y(t) = g[x(t)], (5.6)

где g[x(t)] показывает, что у(t) является функцией x(t). Обозначим координату установившегося состояния через х₀. Раскладываем функцию в окрестности этой точки в ряд Тейлора:

(5.7)

Значение производной характеризует наклон касательной к кривой функции y = g(x) в рабочей точке х₀. Эта касате­льная может служить хорошей аппроксимацией исходной кривой в случае малых значений (x-x₀), то есть отклонения от рабочей точки. В таком предположении можно записать:

,

где т есть тангенс угла наклона касательной к кривой в рабочей точке.

Окончательно урав­нение можно записать в виде

или .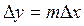

То есть линеаризация уравнения геометрически может трактоваться как замена первоначальной кривой на касательную к ней прямую. Эта замена тем точнее, чем меньшие величины отклонения возникают в исследуемом динамическом процессе (основная предпосылка для линеаризации). Границы отклонений , для которых допустима линеаризация, тем шире, чем ближе кривая к своей касательной. Последним обстоятельством и определяются практически в каждой задаче те границы, внутри которых отклонениям можно считать «достаточно малыми». В ряде задач отличие от линейности бывает столь незначительным, что даже в сравнительно большом диапазоне отклонений можно считать систему линейной. В случае же ярко выраженной нелинейной зависимости линеаризация будет справедлива лишь на соответствующем более узком участке отклонений . Линеаризация может быть совершенно недопустимой при скачкообразных зависимостях. Такого рода зависимости называются существенно нелинейными.

Из геометрической трактовки вытекает более упрощенный метод линеаризации, часто используемый на практике: с самого начала все криволинейные зависимости, используемые при составлении уравнений, заменяются прямолинейными (по касательной в соответствующей точке кривой). Тогда уравнение сразу получается линейным.

Итак, всегда надо помнить, что линейные модели объекта, полученные с помощью процедуры линеаризации, справедливы лишь при малых отклонениях от исходного стационарного режима.

В качестве Ниже приводится примера, иллюстрирующего применение метода линеаризации, рассмотрим колебания маятника длиной L и массой М (см.рисунок).

Момент, действующий на мас­су, равен:

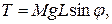(5.12)

где g — ускорение силы тяжести. Условие равновесия маятника соответствует значению .

Зависимость между T и является нелинейной(см.рисунок 5.6(б).

Вычис­ление первой производной в точке равновесия дает линейную аппроксимацию уравнения (5.12) которая имеет вид:

,

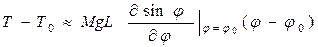где =0. Следовательно, мы имеем

. (5.13)

Эта зависимость является линейной. Подобная аппроксимация является достаточно приемлемой в диапазоне - /4 /4. Напри­мер, колебания линейной модели в диапазоне ±30° от положения равновесия отличаются всего на 2% от действительных колебаний маятника.