Читайте также:
|
Имеем два неизвестных m и σ. Можно показать, что в этом случае доверительным интервалом для m будет интервал (
- 
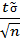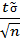; + ), где - выборочное среднее, n – объем выборки, 
- исправленное среднее квадратическое отклонение. = 
, t – находится по таблицам значений функции Стьюдента в зависимости от γ и n (распределение Стьюдента при n →∞ приближается к нормальному). При достаточно больших n (практически при n >20) t можно искать из условия Ф(t) = 
.
Пример. Найти доверительный интервал для математического ожидания нормально распределенной случайной величины Х, для которой по выборке объема n = 25 найдены =2,4 и 
=4, если надежность γ = 0,95. Решение. I способ: t = t (0,95; 25) ≈ 2,064 (по таблицам значений функции Стьюдента). - 
= 2,4 – 
≈ 1,57; + ≈ 3,23 (1,57; 3,23) – доверительный интервал.
II способ: Ф(t) = 0,475 => t ≈ 1,96 => (1,62; 3,18) – доверительный интервал.
Таблица значений функции t = t (γ; n)
| γ n | 0,95 | 0,99 | 0,999 |
| 2,78 | 4,60 | 8,61 | |
| 2,57 | 4,03 | 6,86 | |
| 2,45 | 3,71 | 5,96 | |
| 2,37 | 3,50 | 5,41 | |
| 2,31 | 3,36 | 5,04 | |
| 2,26 | 3,25 | 4,78 | |
| 2,23 | 3,17 | 4,59 | |
| 2,20 | 3,11 | 4,44 | |
| 2,18 | 3,06 | 4,32 | |
| 2,16 | 3,01 | 4,22 | |
| 2,15 | 2,98 | 4,14 | |
| 2,13 | 2,95 | 4,07 | |
| 2,12 | 2,92 | 4,02 | |
| 2,11 | 2,90 | 3,97 | |
| 2,10 | 2,88 | 3,92 | |
| 2,093 | 2,361 | 3,883 | |
| 2,064 | 2,797 | 3,745 | |
| 2,045 | 2,756 | 3,659 | |
| 2,032 | 2,720 | 3,600 | |
| 2,023 | 2,708 | 3,558 | |
| 2,016 | 2,692 | 3,527 | |
| 2,009 | 2,679 | 3,502 | |
| 2,001 | 2,662 | 3,464 | |
| 1,996 | 2,649 | 3,439 | |
| 1,001 | 2,640 | 3,418 | |
| 1,987 | 2,633 | 3,403 | |
| 1,984 | 2,627 | 3,392 |
Дата добавления: 2015-04-20; просмотров: 17 | Поможем написать вашу работу | Нарушение авторских прав |