Читайте также:
|
Система координат на плоскости
А. Основные понятия
Что такое система координат? Это численный способ описания положения точки. Одной из таких систем является прямоугольная (декартова) система координат.
Система из себя представляет две взаимно перпендикулярные прямые (оси координат),имеющие определенный масштаб. Ось Ox - ось абсцисс; ось Oy - ось ординат. Эти две оси делят любую плоскость на четыре области - четверти (или квадраты).
Единичные векторы осе обозначают i и j. Плоскость, в которой распложена система называют координатной плоскостью.
Координаты точки М - координаты радиуса-вектора ОМ. Они имеют вид М(х,у). Х - абсцисса, а У - ордината точки М.
Для определения положения точки используют метод координат. Его сущность состоит в том, что для каждой линии в плоскости сопоставляется ее уравнение.
Есть и иная не менее важная система координат. А именно полярная. Задается она полюсом (точ. О), полярной осью (луч Ор) единичным вектором е сонаправленным с Ор.
Положение точки М определяется радиусом r и углом фи. Эти числа (r and fi) называются полярными числами точки М, обозначают М (r; fi), где r - полярный радиус, fi -полярным углом. r ограничивается отрезком - [0, +бесконечность), а fi - (-pi;pi].
Связь между полярной и декартовой системами координат можно представить в виде:
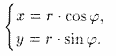
Определяя величину φ, следует установить (по знакам x и у) четверть, в которой лежит искомый угол, и учитывать, что -p < φ< p.
b. Основные приложения метода координат на плоскости.
Дата добавления: 2015-04-20; просмотров: 135 | Поможем написать вашу работу | Нарушение авторских прав |