|
Читайте также: |
Одна книга по геологии пыталась объяснить такое изменение флюорита (Рис.6-36). Внизу справа вы видите куб. Если поровну срезать все его вершины, то это называется огранкой. Можно произвести огранку любого многогранника, то есть любую из этих многогранных форм. Проделывая это (в данном случае с кубом), можно срезать вершины, рёбра или грани, только срезать их надо так, чтобы все срезанные части были одинаковы.
Если произвести огранку этого куба отрезанием всех его вершин под углом в 45 градусов, то получится следующая фигура, находящаяся рядом слева. Если произвести её огранку ещё раз точно таким же образом, то получится опять следующая слева фигура. Проделав это ещё раз, вы получите октаэдр (последний слева). Теперь можно пойти назад другим путём, производя огранку углов октаэдра и проходить через всю эту процедуру до тех пор, пока опять не получится куб. Так в этой книге по геологии пытались пояснить, как же в самом деле флюорит меняет форму. В действительности, книга объясняет только то, как эта перемена могла бы происходить на уровне геометрии. Но в природе, при изменении флюорита имеет место нечто значительно более потрясающее. Чтобы составить другую сетку, на самом деле ионы вращаются и - расширяются или сжимаются!
Вот другой кристалл флюорита (Рис.6-37), один из моих собственных. Он очень велик, около четырёх футов по грани. Сейчас уже не часто увидишь такой большой. На случай, если вам не очень хорошо видно, я скажу, что в центре он поднимается к вершине. Кто-то положил его на подоконник, где на него падал солнечный свет, и - поскольку связи во флюорите так слабы, что когда на него упал солнечный свет - он раскололся, конечно же, вдоль октаэдральных атомных линий.
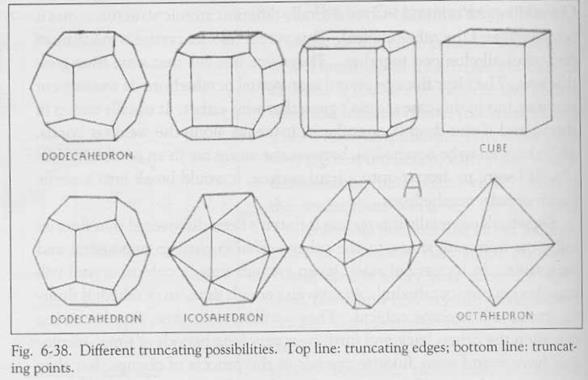
В верхнем правом углу Рис.6-38 находится куб. Следующий слева от него куб огранён по своим рёбрам. Последующая двойная огранка превратила эту латку-перелатку в додекаэдр. Это пример куба/додекаэдра в кристаллах.
На Рис.6-39 верхний кристалл, это куб серного колчедана – пирит. Таким он вырос, никто его не обрабатывал. Есть такой же, как этот, но огромный – в Силверадо, Колорадо, размером, я думаю, где-то около шести квадратных футов. Его просто извлекли из земли в виде совершенного куба. Этот маленький пирит по двумграням квадратен и по остальным 
прямоуголен. Нижний кристалл – это крошечная гроздь пиритовых додекаэдров. Некоторые из них почти совершенны – так они выросли в Перу. Если бы эта маленькая кучка была на достаточно долгое время оставлена в земле, то эти маленькие додекаэдрончики превратились бы в кубики; и по прошествии достаточного количества времени они бы опять стали додекаэдрами. Если взять додекаэдр (внизу слева на Рис.6-38) и произвести огранку его вершины, то он превратится в икосаэдр (рядом справа). Если продолжать огранку вершин, то получится октаэдр. Я могу долго продолжать заниматься этой огранкой. Существует тысячи способов, как это можно проделать. Каждая модель и кристалл, независимо от того, каким бы сложным он ни стал, будет превращаться в одну из пяти Платоновых тел, если вы станете правильно производить его огранку, выявляя 
врождённую природу пяти Платоновых тел в кристаллической структуре.
Маленькая пометка на полях: Если посмотреть внутрь огранённого по вершинам тетраэдра, сделанного из стекла или хрусталя или даже зеркал, то он будет отражать свет. Зеркальное отражение внутри него будет идеальным икосаэдром. Проверьте это.
Так можно продолжать и продолжать. Вы встретите что-то, что выглядит действительно странно, будто это никак не может быть основано на чём-то логическом, но всё, что вам следует сделать, это немного позаниматься геометрией, и каждый раз вы будете обнаруживать, что оно произошло из одной из пяти Платоновых тел. Исключения не известны. Независимо от того, какова модель кристалла, она всегда основана на Платоновом теле. Кристаллические структуры являются деятельностью пяти Платоновых тел, вышедших из Плода Жизни, из Куба Метатрона. Если вы хотите увидеть больше таких кристаллов, можете найти очень много в книге Чарльза А.Соррелла «Камни и Минералы» (Сharles A.Sorell, Rocks and Minerals).
Есть ещё кое-что, о чём я хочу поговорить, вернувшись к Рис.6-38, это «Различные возможности огранки». При огранке октаэдра отрезанием всех вершин так, чтобы срезы оказались под углом в 90 градусов друг относительно друга (показано на фигуре А), получается форма, находящаяся от неё слева. Если нарисовать это на плоскости, то получится квадрат с ромбом посередине (Рис.6-40). Эта модель, как оказывается, связана с нашим сознанием, с самой природой того, чем мы являемся.
Дата добавления: 2015-09-10; просмотров: 52 | Поможем написать вашу работу | Нарушение авторских прав |