Читайте также:
|
С помощью тройного интеграла можно вычислить ряд геометрических и физических величин:
- объем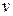 
пространственной области 
находится по формуле 
;
- массу 
тела, занимающего область , можно вычислить с помощью тройного интеграла 
, где 
– плотность распределения массы;
- координаты центра тяжести 
тела, занимающего область , находятся по формулам: 
, 
, 
, где 
– статические моменты тела относительно координатных плоскостей:
, 
, 
.
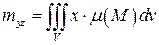Для однородного тела 
;
- моменты инерции тела, занимающего область , относительно координатных осей 
и начала координат 
(полярный момент) определяются формулами:
, 
,
, 
.
ВЕКТОРНЫЙ АНАЛИЗ
В этом разделе рассматриваются элементы дифференциального и интегрального исчисления в векторной форме.
Скалярные и векторные поля
Основные понятия
Пусть 
– область в трехмерном пространстве. Если определена функция 
: 
, то говорят, что в области задано скалярное поле (или скалярная функция ). Таким образом, скалярное поле есть функция трех переменных 
или, что то же, точки 
с координатами 
, 
и 
. Наряду с обозначениями 
или 
используют запись 
, где 
– радиус-вектор точки .
Всюду ниже рассматриваются только гладкие скалярные поля, то есть предполагается, что функция имеет непрерывные частные производные 
, 
, и 
, причем 
для любой точки из области .
Если для любой точки 
ставится в соответствие вектор 
, то говорят, что в области задано векторное поле 
. Если положить 
, то векторное поле можно обозначить так же в виде 
. Таким образом, векторное поле является функцией 
. Векторное поле может быть записано покоординатно в виде 
, где 
, 
, 
– некоторые определенные в функции.
Определенное равенством векторное поле называют непрерывным, если 
и гладким, если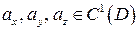 
. Всюду ниже рассматриваются только непрерывные векторные поля.
Аналогичным образом определяются скалярные и векторные поля на плоскости 
.
Дата добавления: 2015-09-10; просмотров: 35 | Поможем написать вашу работу | Нарушение авторских прав |