Пусть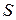 
- замкнутая поверхность, ограничивающая объем 
и 
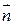- внешняя единичная нормаль к 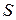. Для наглядности изложения вновь предположим, что рассматривается поток несжимаемой жидкости. Знак 
зависит, очевидно, от величины угла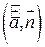 
между 
и 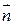: он положительный, если угол 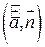острый, и отрицательный, если он тупой.
Говорят, что жидкость вытекает из объема 
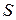в точке поверхности , если в этой точке 
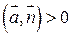, и втекает в объем , если 
.
При таком подходе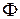 
в формуле есть разность между количествами вытекающей и втекающей жидкости за единицу времени через поверхность 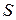. В силу предположения несжимаемости жидкости ее количество постоянно внутри объема .
Пусть 
, тогда из вытекает больше жидкости, чем втекает. Это означает, что внутри существуют источники, питающие поток. При 
внутри существуют стоки, поглощающие жидкость. Понятно, что если в объеме нет ни источников, ни стоков, то 
.
Скалярная величина 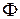в формуле характеризует мощность потока векторного поля (источника, если , и стока, если ) суммарно.
Займемся характеристикой мощности потока в точке 
. С этой целью окружим 
малым объемом 
, целиком лежащим в , и рассмотрим величину
,
где для простоты через 
обозначена величина объема 
, ограниченного замкнутой поверхностью 
. Величина 
характеризует среднюю мощность потока в единице объема, содержащего точку .
Если существует предел , когда стягивается в точку , то его называют дивергенцией (расходимостью) векторного поля в точке и обозначают
.
Из вышеизложенного следует, что в точке имеется источник (сток), если 
(
).
На практике для вычисления 
обычно применяют формулу
,
имеющую место в предположении гладкости поля в точке .
Понятия потока и дивергенции связывает следующее утверждение.
Пусть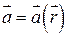 
- гладкое векторное поле в области 
.
Теорема (Гаусса-Остроградского). Поток векторного поля 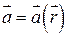через замкнутую поверхность 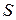в направлении внешней нормали 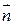равен тройному интегралу по объему , ограниченному поверхностью 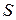, от дивергенции этого векторного поля, т.е.
,
или в развернутом виде
.
Равенство называют формулой Гаусса-Остроградского.
Ротор
В заключение приведем еще одну характеристику векторного поля, называемую ротором поля. При этом для простоты изложения ограничимся приведением лишь формулы для вычисления ротора, не останавливаясь на деталях формального определения с помощью предельного перехода.
Пусть дано гладкое векторное поле 
, определенное в некоторой области 
.
Ротором (или вихрем) векторного поля , обозначаемым 
, называют вектор, вычисляемый по формуле:
.
Дата добавления: 2015-09-10; просмотров: 27 | Поможем написать вашу работу | Нарушение авторских прав |