Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Тогда на том же отрезке с очевидностью .

Эта лемма сохраняет силу и для функций многих переменных.

1.3. Уравнения типа Эйлера и естественные граничные условия. Как убедимся ниже, в задачах линейной теории упругости и строительное механики условие (1.7) обусловлено физически и потому выполняется всегда. Сосредоточим поэтому наше внимание на необходимом условии экстремума функционала (1.6) и покажем, что из него вытекают, так называемые, уравнения типа Эйлера и естественные граничные условия, позволяющие найти такую функцию (значение аргумента функционала), которая доставляет изучаемому функционалу экстремальное значение.

Рассмотрим приращение 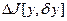простейшего функционала Эйлера (I.I) со свободной границей. Оно, очевидно, представимо в виде

(1.9)

Разлагая здесь в ряд Тейлора функцию , найдем

(1.10)

Здесь введены обозначения

Вспоминая определения и , получим

	(1.11)
	(1.12)

С помощью очевидного тождества

(1.13)

формула (1.11) приводится к виду

(1.14)

Если по условию задачи

(1.15)

где — известные числа, то

(1.16)

и необходимое условие (1.6) экстремума функционала (I.I) принимает вид

(1.17)

Отсюда в силу произвольности 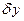и основной леммы вариационного исчисления приходим к уравнению

(1.18)

носящему название уравнение Эйлера.

Нетрудно видеть, что, введя такие очевидные обозначения

и учтено, что , уравнение Эйлера (1.18) можно записать и так

(1.19)

Таким образом, уравнение Эйлера простейшего функционала (I.I) имеет второй порядок. Его общее решение будет содержать две постоянные интегрирования, определяемые из условий (1.15), если таковые предписаны заранее. Если же в условии задачи ограничения (1.15) отсутствуют, то для выполнения необходимого условия (1.6) экстремума функционала (I.I) необходимо, помимо (1.18), потребовать

(1.20)

Эти равенства называются естественными граничными условиями. Они служат для нахождения упомянутых констант в тех случаях, в которых не ставятся условия (1.15).

Итак, чтобы найти функцию, доставляющую экстремум исследуемому функционалу (I.I), нужно построить общее решение уравнения Эйлера (1.18) и выделить из определяемого им семейства функций (их часто называют экстремалями) ту функцию, которая удовлетворяет ограничениям (1.15), если они заданы условием задачи, или естественным граничным условиям, если ограничения (1.15) отсутствуют.

Раскроем теперь необходимое условие экстремума другого функционала

(1.21)

Аналогично предыдущему находим

Это выражение с помощью (1.13) и подобного ему тождества

(1.22)

приводится к виду

(1.23)

Отсюда следует, что 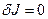тогда, когда 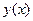является решением уравнения Эйлера

и одновременно удовлетворяет условиям

,

(1.25)

если они предписаны условием задачи, или естественным граничным условиям

,

(1.26)

если ограничения (1.25) отсутствуют.

В заключение приведем без вывода уравнения типа Эйлера

	(1.27)
	(1.28)
	(1.29)

вытекающие из условий стационарности функционалов (1.2), (1.3) и (1.4) соответственно.

1.4. О необходимом условии экстремума функционалов при наличии дополнительных условий. Пусть нас интересует экстремум функционала

(1.30)

с граничными условиями

(1.31)

и дополнительными условиями

(1.32)

Можно показать, что в этом случае уравнения типа Эйлера имеют вид

(1.33)

где

(1.34)

— так называемая функция Лагранжа, а () — множители Лагранжа, определяемые так, чтобы выполнялись уравнения Эйлера (1.33) и дополнительные условия (1.32). Все, сказанное здесь, несложно перенести и обобщить на функционалы более сложной структуры.