При решении практических задач с непрерывными случайными величинами чаще всего приходится сталкиваться со случайными величинами, распределёнными по равномерному, экспоненциальному (показательному) или нормальному законам распределения. Рассмотрим их отдельно.
Равномерное распределение. Непрерывная случайная величина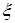 
, принимающая значения на отрезке 
, распределена равномерно на , если плотность распределения 
и функция распределения случайной величины 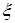имеют соответственно вид
| 
|
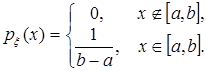
В Mathcad значения в точке 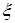плотности распределения и функции распределения случайной величины, имеющей равномерное распределение на отрезке , вычисляются встроенными функциями соответственно dunif(x,a,b) и punif(x,a,b).
Задание 5. Постройте графики плотности и функции распределения равномерного закона на отрезке 
.
Экспоненциальное (показательное) распределение. Непрерывная случайная величина 
имеет показательное распределение с параметром 
, если её плотность распределения имеет вид
Отсюда видно, что показательно распределённая случайная величина принимает только неотрицательные значения. Функция распределения такой случайной величины имеет вид
В MathCAD значения в точке 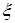плотности распределения и функции распределения случайной величины, имеющей экспоненциальное распределение с параметром 
, вычисляются встроенными функциями соответственно dexp(x, ) и pexp(x, ).
Задание 6. Постройте графики плотности и функции распределения показательного закона с параметром 
.
Нормальное распределение. Это распределение играет исключительно важную роль в теории вероятностей и математической статистике. Случайная величина 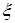нормально распределена с параметрами 
и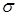 
, 
, если её плотность распределения имеет вид
.
Если случайная величина 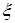имеет нормальное распределение с параметрами и 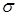, то будем записывать это в виде ~ 
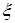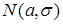. Случайная величина 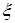имеет стандартное нормальное распределение, если 
и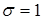 
, ~ 
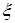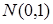. Плотность стандартного нормального распределения имеет вид
,
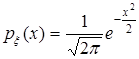а его функция распределения 
, где 
– функция Лапласа:
.
Функция распределения нормальной величины 
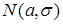~ также выражается через функцию Лапласа: 
.
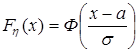В MathCAD значения в точке 
плотности распределения и функции распределения нормальной случайной величины с параметрами , 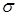вычисляются встроенными функциями соответственно 
и 
.
Задание 7. Постройте графики плотности и функции распределения стандартного нормального закона.
Задание 8. Постройте графики плотности и функции распределения нормального закона с параметрами 
, 
.
Дата добавления: 2015-09-12; просмотров: 17 | Поможем написать вашу работу | Нарушение авторских прав |