
Основным недостатком градиентного метода является необходимость частого вычисления производных от заданной функции. В методе наискорейшего спуска длина шага αk определяется из условия:
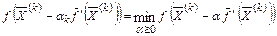 (14.1)
(14.1)
то есть на каждом шаге находится оптимальное значение α, минимизирующее одномерную функцию по направлению антиградиента: один раз вычисляется градиент и ищется минимум по этому направлению.
Для двумерной функции f (x, y) αk определяют следующим образом. После определения градиента минимизируемой функции делается шаг в направлении, обратном градиенту и пропорциональный ему (чем меньше крутизна функции, тем меньше и шаг):
 (14.2)
(14.2)
Если значение целевой функции при этом уменьшилось по сравнению с исходным
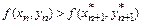 ,
,
то делается очередной рабочий шаг в том же направлении:
 , i = 1, 2, 3,… (14.3)
, i = 1, 2, 3,… (14.3)
ЛАБОРАТОРНАЯ РАБОТА № 13
Поиск экстремумов многомерной функции методом тяжелого шарика
Данный метод базируется на аналогии с движением материального шарика по наклонной поверхности. Шарик будет стремиться занять нижнее положение, то есть точку минимума, со скоростью в зависимости от крутизны наклона, его массы и вязкости среды. Эти параметры влияют на характер движения шарика.
Для двумерной функции траектория поиска в дискретном варианте описывается в соответствии с (13.1).
 , i = 1, 2, 3, … (13.1)
, i = 1, 2, 3, … (13.1)
При α =0 метод превращается в обыкновенный градиентный, при α =1 процесс поиска не затухает. То есть эффективность метода зависит не только от h и начальных условий, но и от 0< α <1. Первый шаг делается обычным методом градиента, так как значение предыдущей точки еще неизвестно.
Варианты заданий приведены в таблице 10 к лабораторной работе №12. Использовать для нечетных вариантов точность ε =10-3, алгоритм оценки частных производных – парные пробы. Для четных вариантов точность ε =10-2, алгоритм оценки частных производных – центральная проба. Так же необходимо ограничить количество шагов на уровне 30-100.
 |


Рис. 2. Блок-схема алгоритма метода половинного деления.
 Для применения этого метода необходимо, чтобы функция на отрезке [ a, b ] содержала только один корень. При нахождении этого корня отрезок [ a, b ] делится пополам, то есть выбирается начальное приближение x = (a + b)/2, затем выбирается тот из отрезков [ a, x ] или [ x, b ], на концах которого функция f (x) имеет противоположенные знаки. Новый отрезок снова делится пополам и так далее, до тех пор, пока длина отрезка, на концах которого функция имеет противоположенные знаки, не будет меньше заданного числа ε. Блок-схема метода приведена на рис. 2.
Для применения этого метода необходимо, чтобы функция на отрезке [ a, b ] содержала только один корень. При нахождении этого корня отрезок [ a, b ] делится пополам, то есть выбирается начальное приближение x = (a + b)/2, затем выбирается тот из отрезков [ a, x ] или [ x, b ], на концах которого функция f (x) имеет противоположенные знаки. Новый отрезок снова делится пополам и так далее, до тех пор, пока длина отрезка, на концах которого функция имеет противоположенные знаки, не будет меньше заданного числа ε. Блок-схема метода приведена на рис. 2.
1.4. Метод Ньютона
Метод Ньютона (метод касательных) состоит в том, что приближенным значением корня  считается точка пересечения касательной к кривой f (x) и оси 0 X (рис. 3).
считается точка пересечения касательной к кривой f (x) и оси 0 X (рис. 3).

Рис. 3. Корень уравнения, определенный методом Ньютона.
Для применения метода необходимо:
а) чтобы на отрезке [ a, b ] производная f '(x) была всюду отлична от нуля;
б) чтобы функция f (x) была на [ a, b ] монотонна (производная сохраняла знак);
 |
| № | Функция | Начальное приближение | |

| -4 | -1 | |
| 0.5 | 0.5 | |

| -5 | -5 | |

| -1 | -1 | |

| -4 | ||

| -0.9 | -0.3 | |
| 1.5 | 1.3 | |

| -1 |
 № №
| Функция | Начальное приближение | |

| 0.5 | 2.6 | |

| -2 | ||
| |||

| -4 | ||

| -1.2 | -1.9 | |

| 1.5 | 1.3 | |
| |||

|
в) в качестве начального приближения следует выбирать такую точку x 0, для которой выполняется условие f (x 0 ) ∙ f '' (x 0) > 0 (то есть точку, в которой кривизна и функция имеют одинаковые знаки).
Рабочая формула метода
 (1.4)
(1.4)
позволяет найти последовательность x 0, x 1, x 2, …, xn, сходящуюся к точному значению корня ξ уравнения (1.1). Критерием окончания вычислительного процесса является выполнение условия:
| x n +1 - x n | < ε.
Алгоритм метода
1. Выбрать начальное приближение x 0, принадлежащее промежутку [ a, b ], положить x = x 0.
2. Вычислить 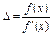 .
.
3. Если |Δ| < ε, то корень ξ = x -Δ, вычисления окончены.
4. Положить x = x -Δ и вернуться к шагу 2.
1.5. Метод итераций
Метод итераций (последовательных приближений) предполагает, что уравнение (1.1) преобразовано к виду:
x = φ (x). (1.5)
Последовательные приближения корня x 0, x 1, x 2, … задаются рабочей формулой:
xn +1 = φ (xn) при n = 0, 1, 2, … (1.6)
Последовательность x 0, x 1, x 2, …, xn, … сходится к точному значению корня ξ, если для любого x Î [ a, b ] выполнено условие сходимости метода:
| φ ' (x)| < 1 (1.7)
Алгоритм метода
1. Выбрать начальное приближение x Î [ a, b ].
2. Вычислить Δ = φ (x).
 |
 4. Положить x = Δ и перейти к шагу 2.
4. Положить x = Δ и перейти к шагу 2.

Рис. 4. Последовательное нахождение корня методом итераций.
Вопрос о преобразовании уравнения (1.1) к виду (1.5) решается в каждом отдельном случае по своему. В общем случае можно рекомендовать некоторый универсальный, но довольно громоздкий прием. Если ищется корень уравнения f (x) = 0на отрезке [ a, b ], то необходимо найти число
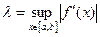 , (1.8)
, (1.8)
равное значению точной верхней границы модуля производной функции f (x)на отрезке [ a, b ]. Тогда φ (x) можно выбрать в виде:
 ; (1.9)
; (1.9)
при этом условие сходимости (1.7) выполняется автоматически.
Варианты заданий приведены в табл. 1. Для всех заданий принять точность вычислений ε = 10-5.
 |
| № | Функция | Начальное приближение | |

| -3 | ||

| -4 | ||

| -2.1 | 0.05 | |

| -2 | -1.2 | |

| |||

| -2.5 | -0.5 | |

| 0.8 | -5 |
 Таблица 10. Варианты заданий к лабораторной работе № 12.
Таблица 10. Варианты заданий к лабораторной работе № 12.
| № | Функция | Начальное приближение | |
| х0 | у0 | ||

| -1.25 | -1.95 | |

| -2.5 | 5.2 | |

| -2 | ||

| -3 | -3 | |

| -4 | ||
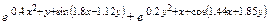
| -2.5 | 0.2 | |

| -1 |
 |
Таблица 1. Варианты заданий к лабораторной работе № 1.
| № вар. | Уравнение | Отрезок, содержащий корень | Метод численного решения |

| [2;3] | итераций | |

| [0;2] | Ньютона | |

| [0,4;1] | половинного деления | |
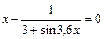
| [0;0,85] | итерация | |

| [1;2] | Ньютона | |

| [0;0,8] | половинного деления | |

| [0;1] | итераций | |

| [2;4] | Ньютона | |

| [1;2] | половинного деления | |

| [0;1] | итераций | |

| [0;1] | Ньютона | |

| [1;3] | половинного деления | |

| [1,2;2] | итераций | |

| [3;4] | Ньютона | |

| [1;2] | половинного деления |
 № вар. № вар.
| Уравнение | Отрезок, содержащий корень | Метод численного решения |

| [0;1,5] | итераций | |

| [1;3] | Ньютона | |

| [0;1] | половинного деления | |

| [0,5;1] | итераций | |

| [1;3] | Ньютона | |

| [0;1] | половинного деления | |

| [2;3] | итераций | |

| [0,4;1] | Ньютона | |

| [-1;0] | половинного деления | |

| [2;3] | итераций | |

| [0,2;1] | Ньютона | |

| [1;2] | половинного деления | |

| [1;2] | итераций | |
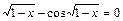
| [0;1] | Ньютона | |

| [2;3] | половинного деления |

Таблица 9. Пример вывода результатов к работе № 12.
| № | x | y | df/dx | df/dy | |grad f(x,y)| | f(x,y) |
| 0.5000 | 0.5000 | 0.8776 | 0.8776 | 1.2411 | 0.4794 | |
| 0.2367 | 0.2367 | 0.4705 | 0.4705 | 0.6654 | 0.1118 | |
| 0.0956 | 0.0956 | 0.1911 | 0.1911 | 0.2703 | 0.0183 | |
| 0.0382 | 0.0382 | 0.0765 | 0.0765 | 0.1082 | 0.0029 | |
| 0.0153 | 0.0153 | 0.0306 | 0.0306 | 0.0433 | 0.0005 | |
| 0.0061 | 0.0061 | 0.0122 | 0.0122 | 0.0173 | 0.0001 | |
| 0.0024 | 0.0024 | 0.0049 | 0.0049 | 0.0069 | 0.0000 | |
| 0.0010 | 0.0010 | 0.0020 | 0.0020 | 0.0028 | 0.0000 | |
| 0.0004 | 0.0004 | 0.0008 | 0.0008 | 0.0011 | 0.0000 | |
| 0.0002 | 0.0002 | 0.0003 | 0.0003 | 0.0004 | 0.0000 |
Использовать для четных вариантов точность ε =10-3, алгоритм оценки частных производных – парные пробы. Для нечетных вариантов точность ε =10-2, алгоритм оценки частных производных – центральная проба. Варианты заданий приведены в таблице 9.
Величина рабочего шага в направлении антиградиента зависит как от самого градиента, так и от коэффициента пропорциональности h, с помощью которого можно управлять эффективностью метода. Существуют разновидности метода как с постоянным, так и с переменным шагом. Последние здесь не рассматриваются.
 Для оценки частных производных в общем случае используются разные методы с двумя вариантами:
Для оценки частных производных в общем случае используются разные методы с двумя вариантами:
1. Алгоритм с центральной пробой
 .
.
2. Алгоритм с парными пробами
 ,
,
где gi – пробный шаг по i -ой переменной, выбираемый достаточно малым для разностной оценки производной.
Условием окончания поиска минимума может являться условие, когда величина модуля градиента менее заданной точности ε.
Пример
Требуется найти минимум функции

с заданными начальными координатами х = 0.5; y = 0.5 и точностью вычислений ε =10-3.
Зададимся значениями пробного шага g =10-3 и коэффициента шага h =0.3. Обычно данный коэффициент приходится подбирать вручную. Так, при h =0.1 минимум находится за 32 шага, а при h =1 процесс не сходится. Поэтому надо вводить вторую проверку окончания цикла: по количеству приближений.
Если выводить промежуточные результаты вычислений, то получим следующую таблицу:
 |
ЛАБОРАТОРНАЯ РАБОТА № 2
Отделение и уточнение корней нелинейных уравнений
Данная работа аналогична работе №1 с той разницей, что здесь задан ориентировочный участок функции, где могу быть один или несколько корней. Поэтому необходимо сначала отделить и определить достаточно малый участок, где есть корень, методом проб, а затем уточнить значение корня быстросходящимся методом. Так как корней на заданном участке может быть несколько, например, как показано на рис. 5, то после уточнения корня необходимо проверять наличие корней и далее до конца участка.
При выполнении задания для метода проб отрезок предлагается делить на 20 частей. Из-за сложности анализа функций на сходимость для уточнения корней использовать метод половинного деления с заданной точностью.

Рис. 5. Отделение корней нелинейного уравнения.
Блок-схема алгоритма приведена на рис. 6, варианты заданий в таблице 2.

 Рис. 6. Блок-схема алгоритма отделения и уточнения корней уравнения.
Рис. 6. Блок-схема алгоритма отделения и уточнения корней уравнения.

Дата добавления: 2015-09-12; просмотров: 57 | Поможем написать вашу работу | Нарушение авторских прав |