E)жинақсыз
F)жинақсыз, өйткені q =3
функциясынының х = 0 нүктедегі екінші ретті туындысы: С)оң сан D)25E)бүтін сан
функциясының х 
= -1 нүктесіндегі туындысын табу керек: D)6E)24/4F)0.6*10
2х + у – 7 = 0 түзуінде жатқан нүкте: С)(1;5)Е)(0;7)
А(2,2) және В(5,-2) нүктелері берілген.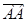 
векторының ординатасы: Д)-4
Анықтауышты есепте: 
Е)20/2;Ғ)30/3
Бірінші ретті сызықтық дифференциалдық теңдеу: В)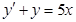 
С) 
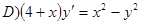
Векторлардың компланарлық шарты: А)Осы векторлардан құралған параллелпипедтің көлемі кез-келген оң санға теңД)Аралас туынды нөлге тең, аралас көбейтінді нөлге тең
Даламбер белгісі бойынша қатар 
С)жинақты, өйткені q 
Е)жинақты
Е)12/3Ғ)4
Есепте: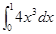 
А)0,1*10С)10 
Есепте: 
Ғ) 
М (1;-2) нүктесінде 
- нің мәні, егер Z=5ху - 
:А) 
D) 
E) 
матрицасын табу керек: D)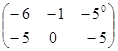 
Е) 
Ғ) 
С= 
матрицасын табу керек: В) 
Сызықтармен шектелген фигураның ауданын табу керек:
Шекті есепте: 
В)6/3
Шекті есепте: 
А)1/2В)4/8
шеңберінің радиусы неге тең: С)6/2Д)9/3G)3
Дата добавления: 2014-11-24; просмотров: 72 | Поможем написать вашу работу | Нарушение авторских прав |