Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Трифилярный подвес.

1. Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена 2013 года по информатике и ИКТ (проект).
2. Ал.А. Марков, Введение в теорию кодирования. — М.: Наука, 1982.
3. С.В. Яблонский, Введение в дискретную математику. — М.: Наука, 2000.
4. Л.П. Жильцова. Современные проблемы теории кодирования. Учебно-методические материалы по программе повышения квалификации «Информационные технологии и компьютерное моделирование в прикладной математике». — Нижний Новгород: 2007.
5. Л.П. Жильцова, Т.Г. Смирнова. Основы теории графов и теории кодирования в примерах и задачах: Учебное пособие. — Нижний Новгород: Издательство Нижегородского госуниверситета, 2008.

Экспериментальная часть.

Трифилярный подвес.

Трифилярный подвес (рисунок 1) представляет собой круглую платформу 1, подвешенную на тр.х симметричных нитях 2, прикрепл.нных к диску меньшего радиуса 3 (рис 1).

Положение платформы при крутильных колебаниях (рис 2).

Упражнение 1. Определение момента инерции платформы.

1. Движение ручки 4 вниз заставляет крутиться платформу.

2. Измеряем 10 полных оборотов платформы (n) за 10 секунд (t).

3. Рассчитываем значение периода колебаний пустой платформы по формуле:

T₀=

4. Рассчитаем момент инерции пустой платформы по формуле:

J₀= T₀².

Где M=1.025 кг, g=9.8, R=0.2 м, r=0.045 м, l=1.77 м

5. Так как платформа представляет собой диск, то рассчитаем теоретическое значение момента её инерции по формуле:

J₀^теор= MR².

6. Рассчитаем и занесем результаты в таблицу 1.

T₀= =4.063333

J₀= *4.063333²=0.021444

J₀^т= =0,0205

7. Сравним J₀ и J₀^теор: J₀≈0.02, J₀^теор≈0,02. То есть J₀≈J₀^теор

Упражнение 2. Проверка теоремы Штейнера.

1. Расположим один над другим 3 груза, в центре платформы.

2. Снова измеряем время за 10 полных оборотов платформы.

3. Вычислим период колебаний T₁ и рассчитаем момент инерции по формуле:

J₁= 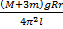T₁²

4. Рассчитаем и занесем результаты в таблицу 2.

T₁= =2.92

J₁= 2.92²=0.019031

5. Расположим грузы на одинаковом расстоянии a от центра платформы и вновь по результатам трех измерений времени колебаний определяем момент инерции платформы с грузами по формуле:

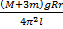J₂= T₂²

6. Рассчитаем и занесем результаты в таблицу 3.

T₂= =4.25

J₂= 4.25²=0.040304

7. Найдем ∆J:

∆J=J₂-J₁

∆J=0,040304-0,019031=0,021273.

8. С целью проверки теоремы Штейнера сравнить полученное значение ∆J с величиной 3· ma ².

∆J=0,021273, 3ma²=3*0.247*0.16²=0,024008. => ∆J≈0,02, 3ma²=0.02 => ∆J≈3ma²

Контрольные вопросы.

1. Момент инерции материальной точки массой m относительно произвольной оси определяется как произведение массы на квадрат расстояния r от оси до точки.

2. Моментом инерции твердого тела относительно оси называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до оси.

3. Для этого элементы объема тела. V уменьшают до тех пор, пока не будет получен физически малый объем dV с массой dm. Тогда задача определения момента инерции сводится к интегрированию:

J=∫r²dm.

4. Если масса тела распределена по объему с постоянной плотностью., то момент инерции можно представить в виде:

J=ρ∫_vr²dV.

где интегрирование производится по всему объему тела. Так, для сплошного цилиндра радиуса R относительно оси, совпадающей с осью цилиндра, момент инерции:

J= mR².

5. Практическое значение теоремы Штейнера заключается в том, что вычислив значение J_c, значение момента инерции относительно любой другой параллельной оси легко определить по формуле:

J=J_c+ma².

6. Платформа может совершать крутильные колебания вокруг вертикальной оси, перпендикулярной к ее плоскости и проходящей через ее середину. При этом платформа будет совершать колебательные движения и по вертикали. Период колебаний определяется величиной момента инерции платформы. Для возбуждения колебаний служит ручка со шнуром, привязанным к верхнему диску. После возбуждения колебаний верхний диск остается неподвижным.